2.4 — Costs of Production — Class Content

Contents

Overview

Today we cover costs before we put them together next class with revenues to solve the firm’s (first stage) profit maximization problem. While it seems we are adding quite a bit, and learning some new math problems with calculating costs, we will practice it more next class, when put together with revenues.

Readings

Slides

Assignments

Appendix

The Relationship Between Returns to Scale and Costs

There is a direct relationship between a technology’s returns to scaleIncreasing, decreasing, or constant

 and its cost structure: the rate at which its total costs increaseAt a decreasing rate, at an increasing rate, or at a constant rate, respectively

 and its marginal costs changeDecreasing, increasing, or constant, respectively

. This is easiest to see for a single input, such as our assumptions of the short run (where firms can change \(l\) but not \(\bar{k})\):

\[q=f(\bar{k},l)\]

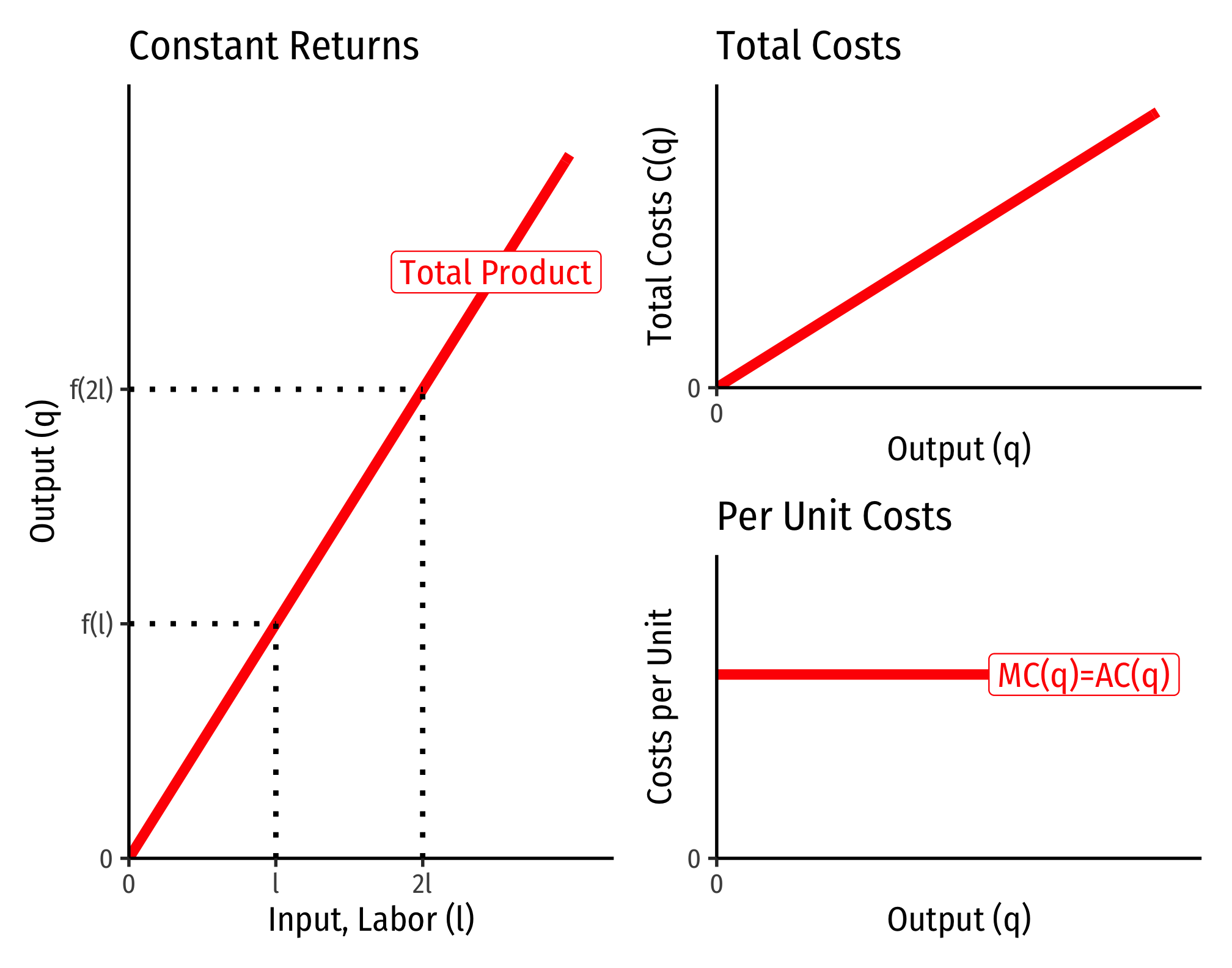
Constant Returns to Scale:

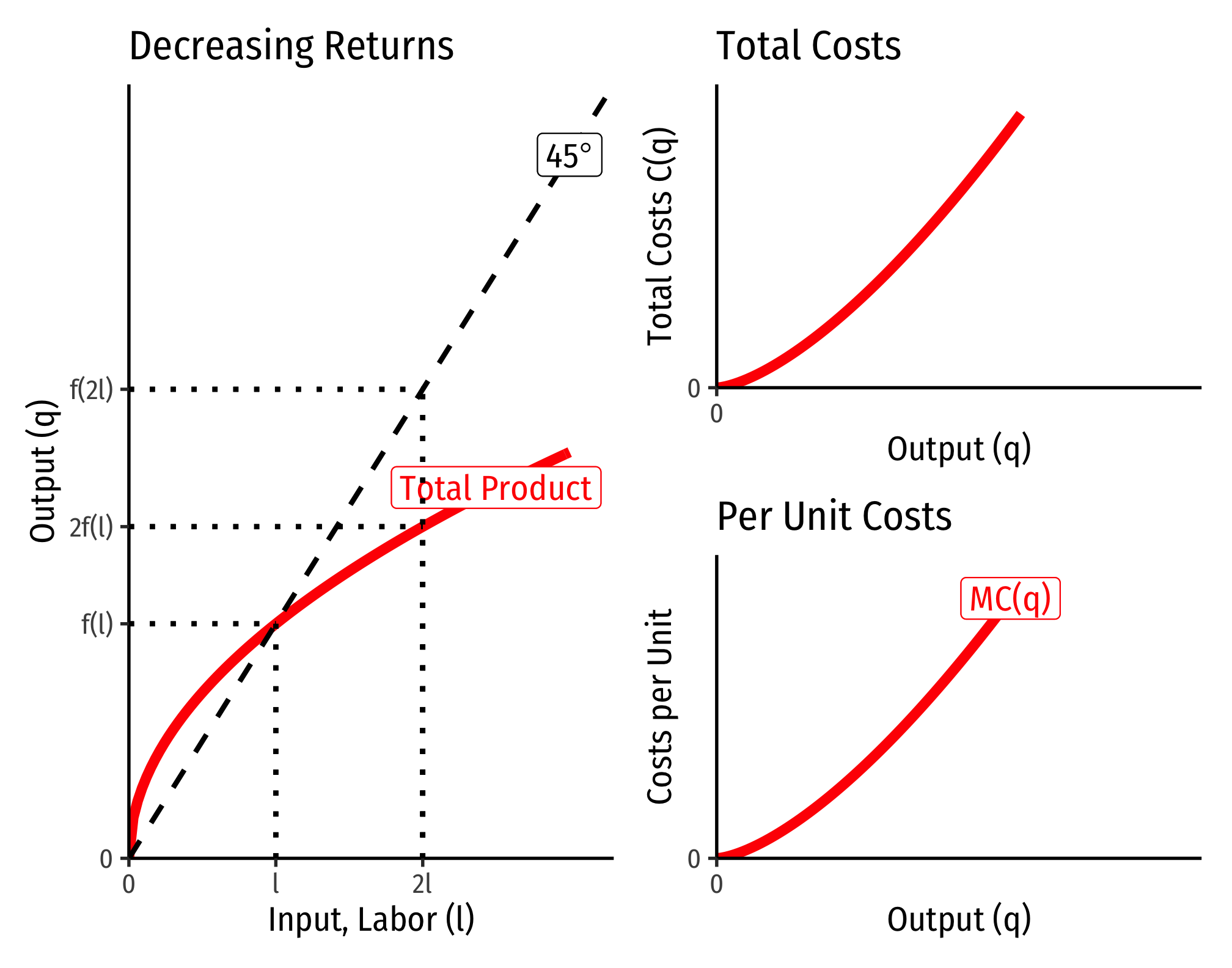
Decreasing Returns to Scale

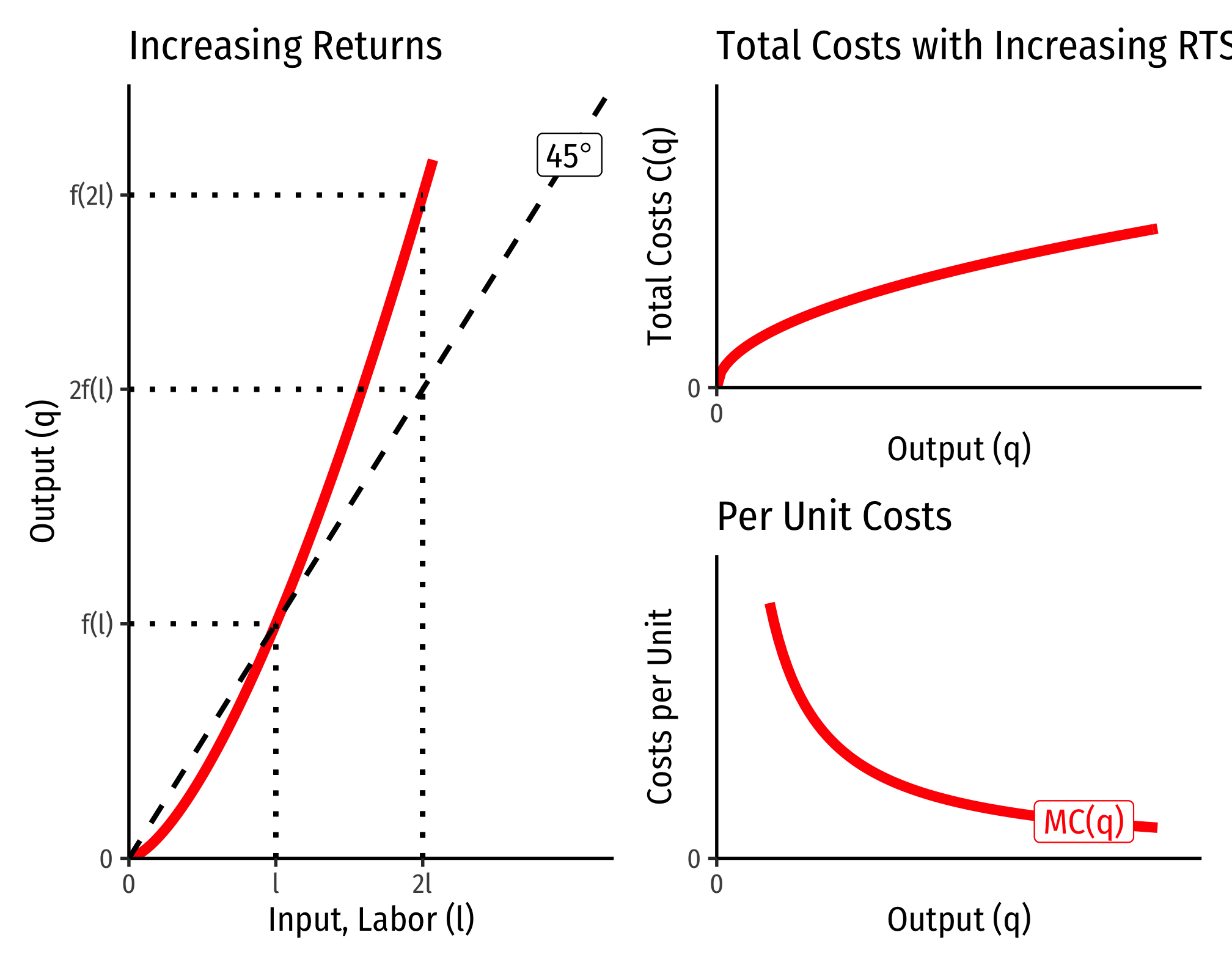
Increasing Returns to Scale

Cobb-Douglas Cost Functions

The total cost function for Cobb-Douglas production functions of the form \[q=l^{\alpha}k^{\beta}\] can be shown with some very tedious algebra to be:

\[C(w,r,q)=\left[\left(\frac{\alpha}{\beta}\right)^{\frac{\beta}{\alpha+\beta}} + \left(\frac{\alpha}{\beta}\right)^{\frac{-\alpha}{\alpha+\beta}}\right] w^{\frac{\alpha}{\alpha+\beta}} r^{\frac{\beta}{\alpha+\beta}} q^{\frac{1}{\alpha+\beta}}\]

If you take the first derivative of this (to get marginal cost), it is:

\[\frac{\partial C(w,r,q)}{\partial q}= MC(q) = \frac{1}{\alpha+\beta} \left(w^{\frac{\alpha}{\alpha+\beta}} r^{\frac{\beta}{\alpha+\beta}}\right) q^{\left(\frac{1}{\alpha+\beta}\right)-1}\]

How does marginal cost change with increased output? Take the second derivative:

\[\frac{\partial^2 C(w,r,q)}{\partial q^2}= \frac{1}{\alpha+\beta} \left(\frac{1}{\alpha+\beta} -1 \right) \left(w^{\frac{\alpha}{\alpha+\beta}} r^{\frac{\beta}{\alpha+\beta}}\right) q^{\left(\frac{1}{\alpha+\beta}\right)-2}\]

Three possible cases:

  1. If \(\frac{1}{\alpha+\beta} > 1\), this is positive \(\implies\) decreasing returns to scale
  1. If \(\frac{1}{\alpha+\beta} < 1\), this is negative \(\implies\) increasing returns to scale
  1. If \(\frac{1}{\alpha+\beta} = 1\), this is constant \(\implies\) constant returns to scale

Example (Constant Returns)

Let \(q=l^{0.5}k^{0.5}\).

\[\begin{align*} C(w,r,q)&=\left[\left(\frac{0.5}{0.5}\right)^{\frac{0.5}{0.5+0.5}} + \left(\frac{0.5}{0.5}\right)^{\frac{-0.5}{0.5+0.5}}\right] w^{\frac{0.5}{0.5+0.5}} r^{\frac{0.5}{0.5+0.5}} q^{\frac{1}{0.5+0.5}}\\ C(w,r,q)&= \left[1^{0.5}+1^{-0.5} \right]w^{0.5}r^{0.5}q^{0.5}\\ C(w,r,q)&= w^{0.5}r^{0.5}q^{1}\\ \end{align*}\]

Consider input prices of \(w=\$9\) and \(r=\$25\):

\[\begin{align*}C(w=9,r=25,q)&=9^{0.5}25^{0.5}q \\ & =3*5*q\\ & =15q\\\end{align*}\]

That is, total costs (at those given input prices, and technology) is equal to 15 times the output level, \(q\):

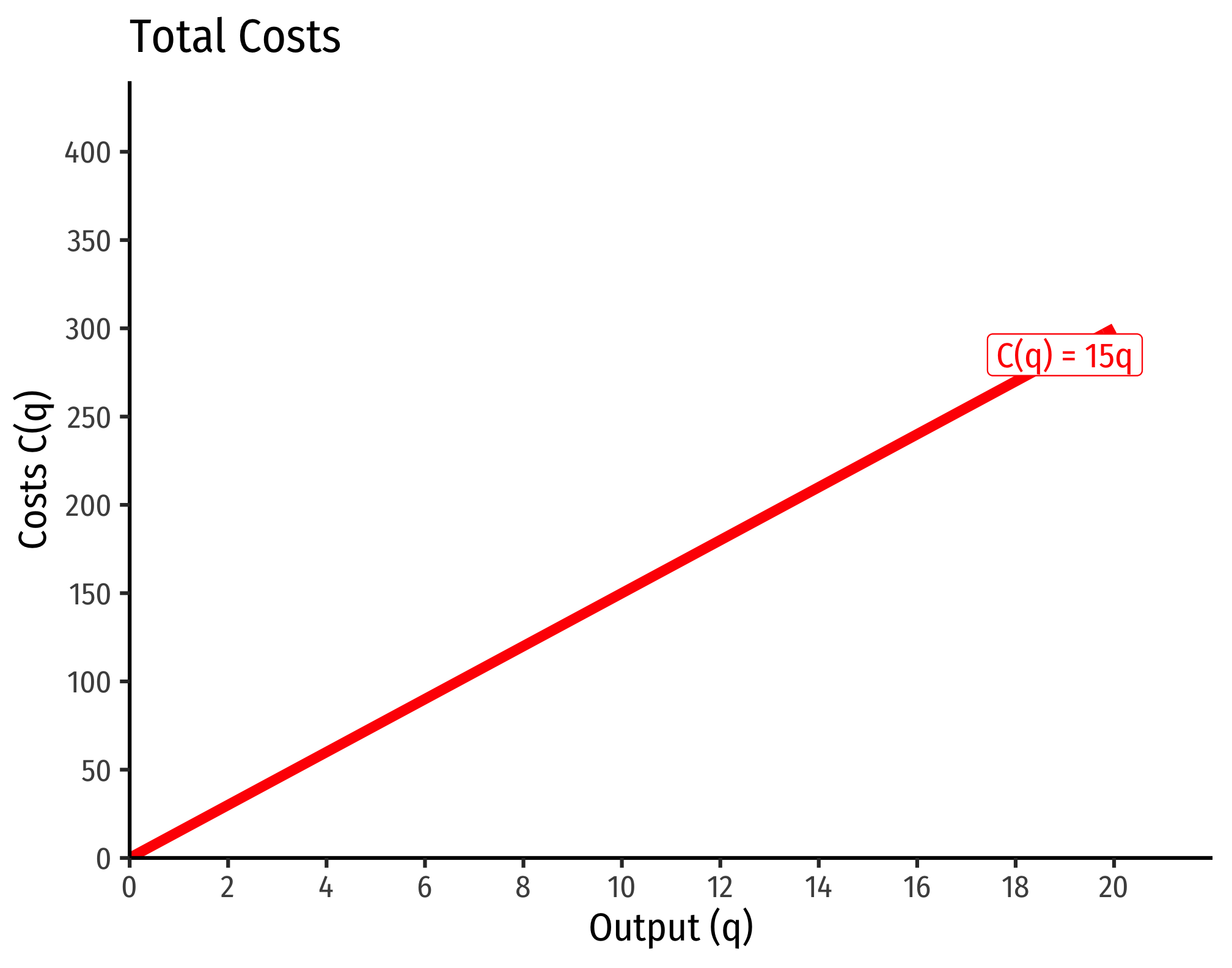
Marginal costs would be

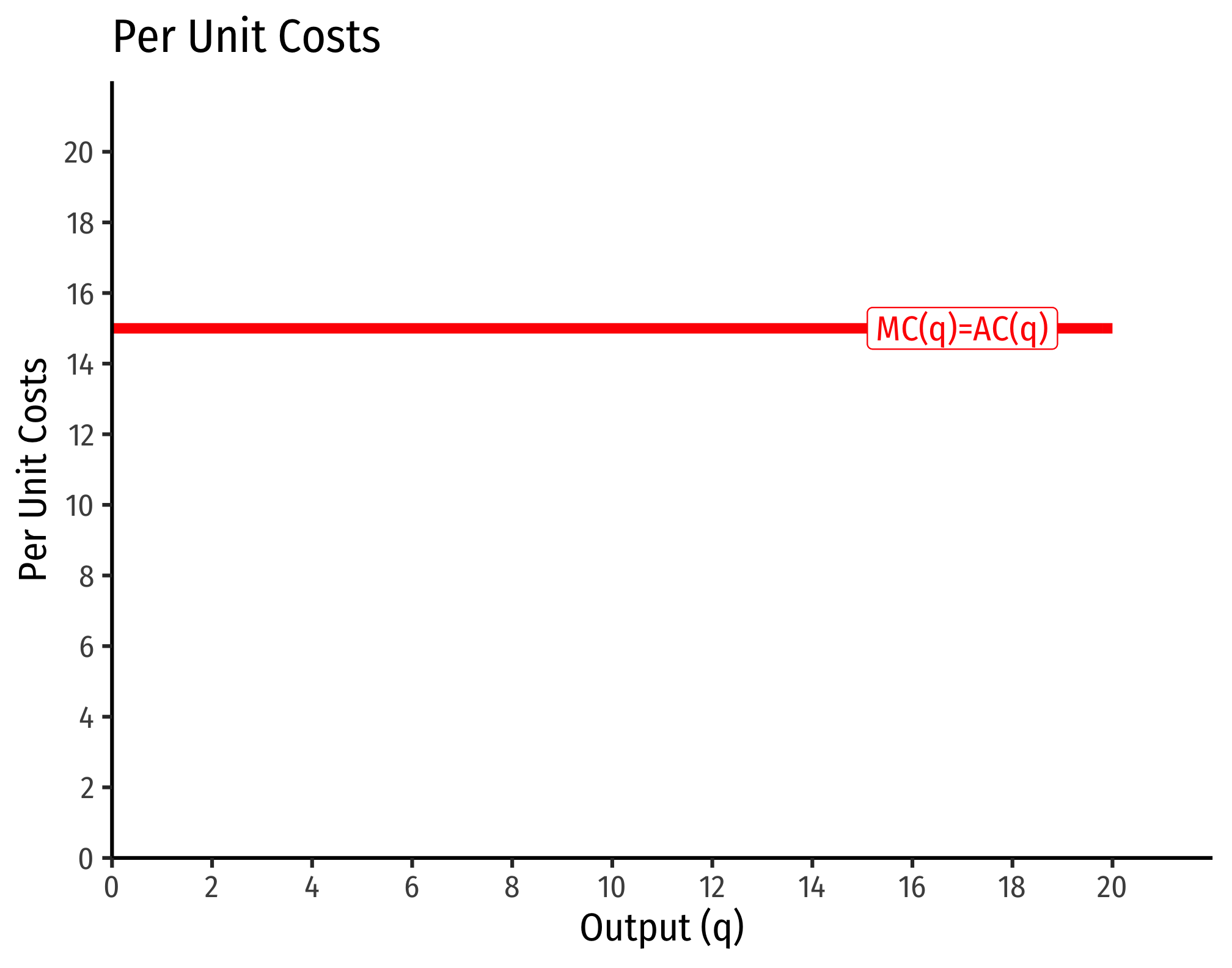
\[MC(q) = \frac{\partial C(q)}{\partial q} = 15\]

Average costs would be

\[MC(q) = \frac{C(q)}{q} = \frac{15q}{q} = 15\]

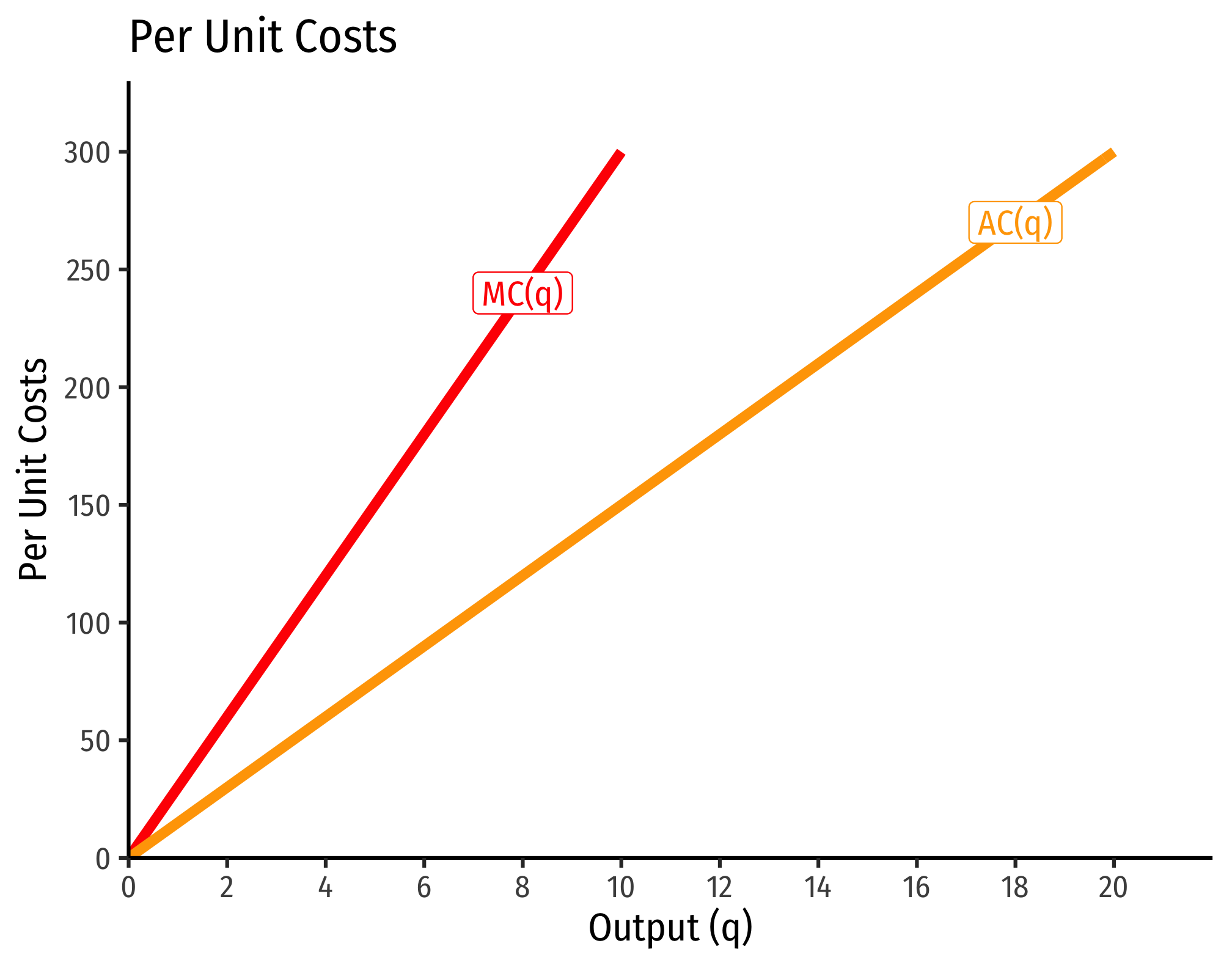
Example (Decreasing Returns)

Let \(q=l^{0.25}k^{0.25}\).

\[\begin{align*} C(w,r,q)&=\left[\left(\frac{0.25}{0.25}\right)^{\frac{0.25}{0.25+0.25}} + \left(\frac{0.25}{0.25}\right)^{\frac{-0.25}{0.25+0.25}}\right] w^{\frac{0.25}{0.25+0.25}} r^{\frac{0.25}{0.25+0.25}} q^{\frac{1}{0.25+0.25}}\\ C(w,r,q)&= \left[1^{0.5}+1^{-0.5} \right]w^{0.5}r^{0.5}q^{2}\\ C(w,r,q)&= w^{0.5}r^{0.5}q^{2}\\ \end{align*}\]

If \(w=9\), \(r=25\):

\[\begin{align*}C(w=9,r=25,q)&=9^{0.5}25^{0.5}q^2 \\ & =3*5*q^2\\ & =15q^2\\\end{align*}\]

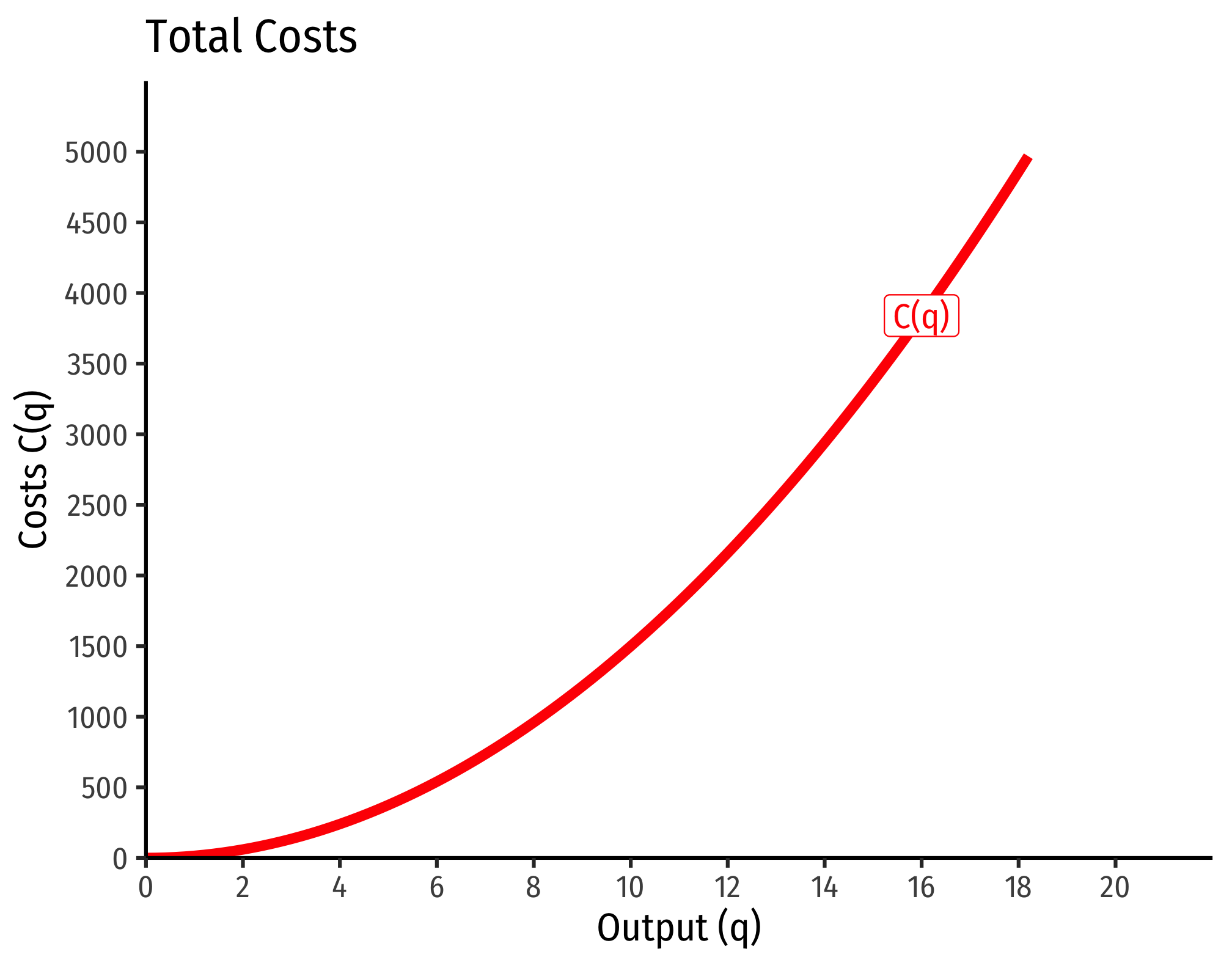
Marginal costs would be

\[MC(q) = \frac{\partial C(q)}{\partial q} = 30q\]

Average costs would be

\[AC(q) = \frac{C(q)}{q} = \frac{15q^2}{q} = 15q\]