2.1 — Production, Specialization, Firms

# 2.1 — Production, Specialization, Firms
## ECON 306 • Microeconomic Analysis • Spring 2021
### Ryan Safner Assistant Professor of Economics <a href="mailto:safner@hood.edu">safner@hood.edu</a> <a href="https://github.com/ryansafner/microS21">ryansafner/microS21</a> <a href="https://microS21.classes.ryansafner.com"> microS21.classes.ryansafner.com</a>

---

# Outline

### [Production, Specialization, & Comparative Advantage](#6)
### [What Do Firms Do?](#32)
---

# Producer Behavior

- How do **producers** decide:
    - which products to produce
    - in what quantity
    - using which resources
    - and for what price?

- Answers to these questions are building blocks for **supply curves**	
]

---

# The Basics of Production

- Nearly all goods must be **produced** before we can exchange & consume them

- .hi[Consumption] is the **destruction** of value to gain utility
    - Consumption is the ultimate goal of all economic activity
]

---

# The Basics of Production

- .hi[Production] is the **creation** of value, by transforming *lower*-valued goods (resources, inputs, etc) into *higher*-valued goods (outputs, consumer products, etc)
]

---

# Production, Specialization, & Comparative Advantage

---

# Production, Specialization, & Comparative Advantage

- Consider a simple example — Robinson Crusoe stranded on a deserted island

- Anything he wants to consume, he must first produce
]

---

# Production, Specialization, & Comparative Advantage

- Suppose on this tropical island, there is the potential to farm two goods:
  - Bananas
  - Coconuts

]

---

# Production, Specialization, & Comparative Advantage

|    | Max Bananas | Max Coconuts |
|----|------------:|-------------:|
| .blue[Plot A] | 10 | 5 |
| .green[Plot B] | 45 | 15 |

]

---

# Production, Specialization, & Comparative Advantage

|    | Max Bananas | Max Coconuts |
|----|------------:|-------------:|
| .blue[Plot A] | 10 | 5 |
| .green[Plot B] | 45 | 15 |

- For each plot, the .hi[(opportunity) cost] of producing a marginal unit:.magenta[†]

|    | 1 Banana | 1 Coconut |
|----|---------:|----------:|
| .blue[Plot A] | 0.5C | 2B |
| .green[Plot B] | 0.33C | 3B |

]

.pull-right[
.center[
![](../images/crusoe.jpg)
]
.footnote[.magenta[†] In other words, the .hi[marginal cost]!]

]

---

# Production, Specialization, & Comparative Advantage

|    | Max Bananas | Max Coconuts |
|----|------------:|-------------:|
| .blue[Plot A] | 10 | 5 |
| .green[Plot B] | 45 | 15 |

- For each plot, the .hi[(opportunity) cost] of producing a marginal unit:.magenta[†]

|    | 1 Banana | 1 Coconut |
|----|---------:|----------:|
| .blue[Plot A] | 0.5C | 2B |
| .green[Plot B] | 0.33C | 3B |

]

]

---

# Production, Specialization, & Comparative Advantage

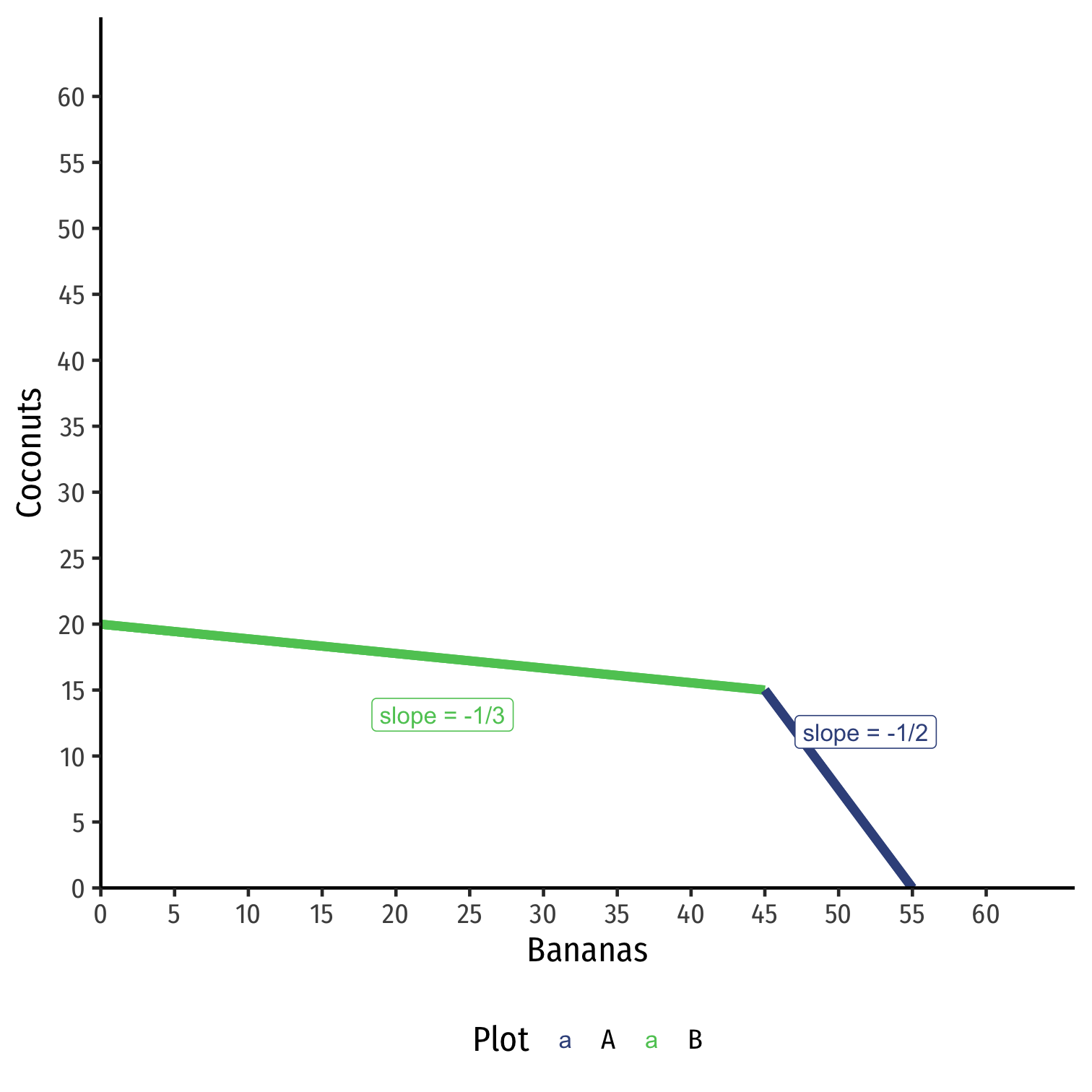
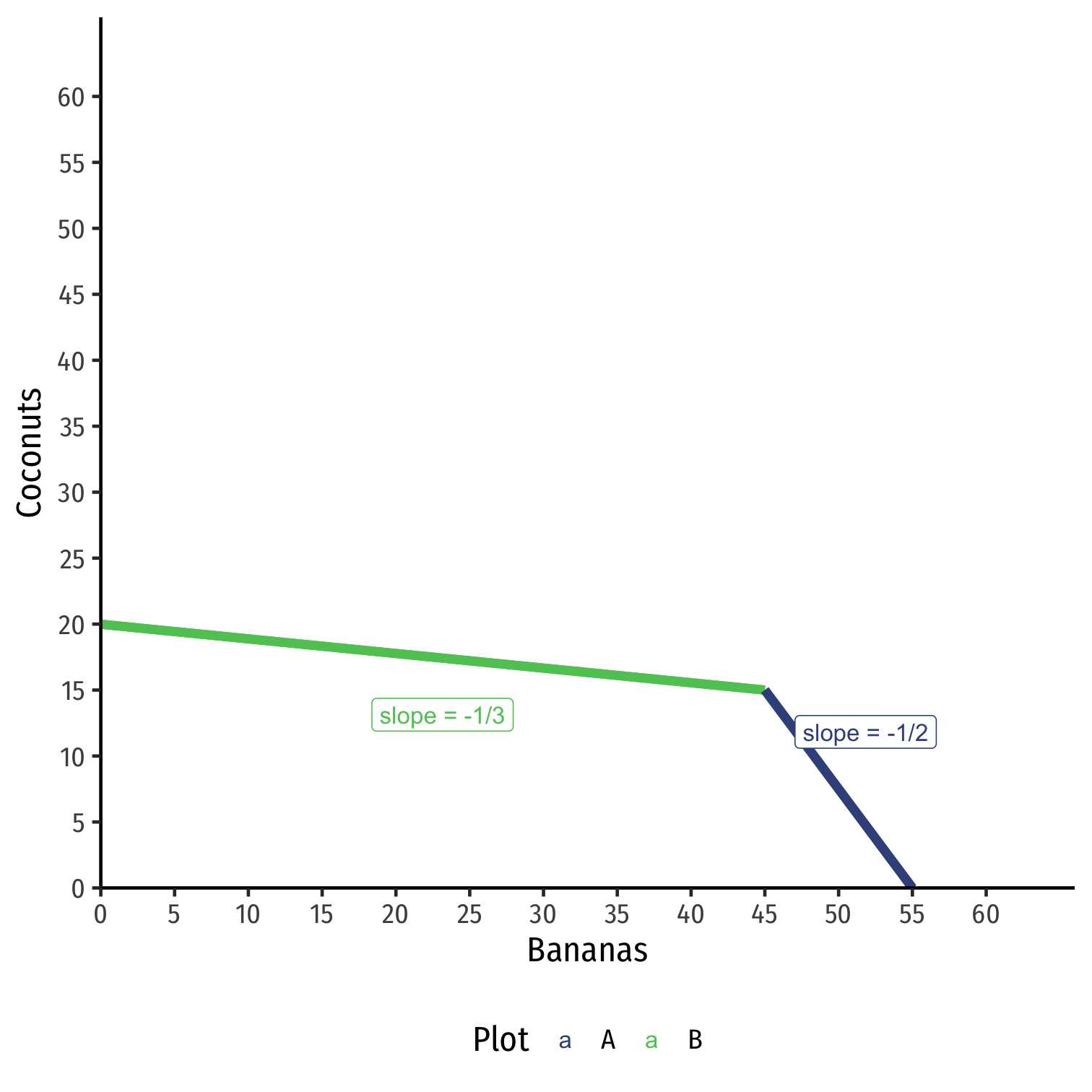
- .hi[Production possibilities frontier (PPF)] displaying possible combinations of outputs

- Slope called .hi[marginal rate of transformation (MRT)], or just call it .hi[marginal cost]

]

]

---

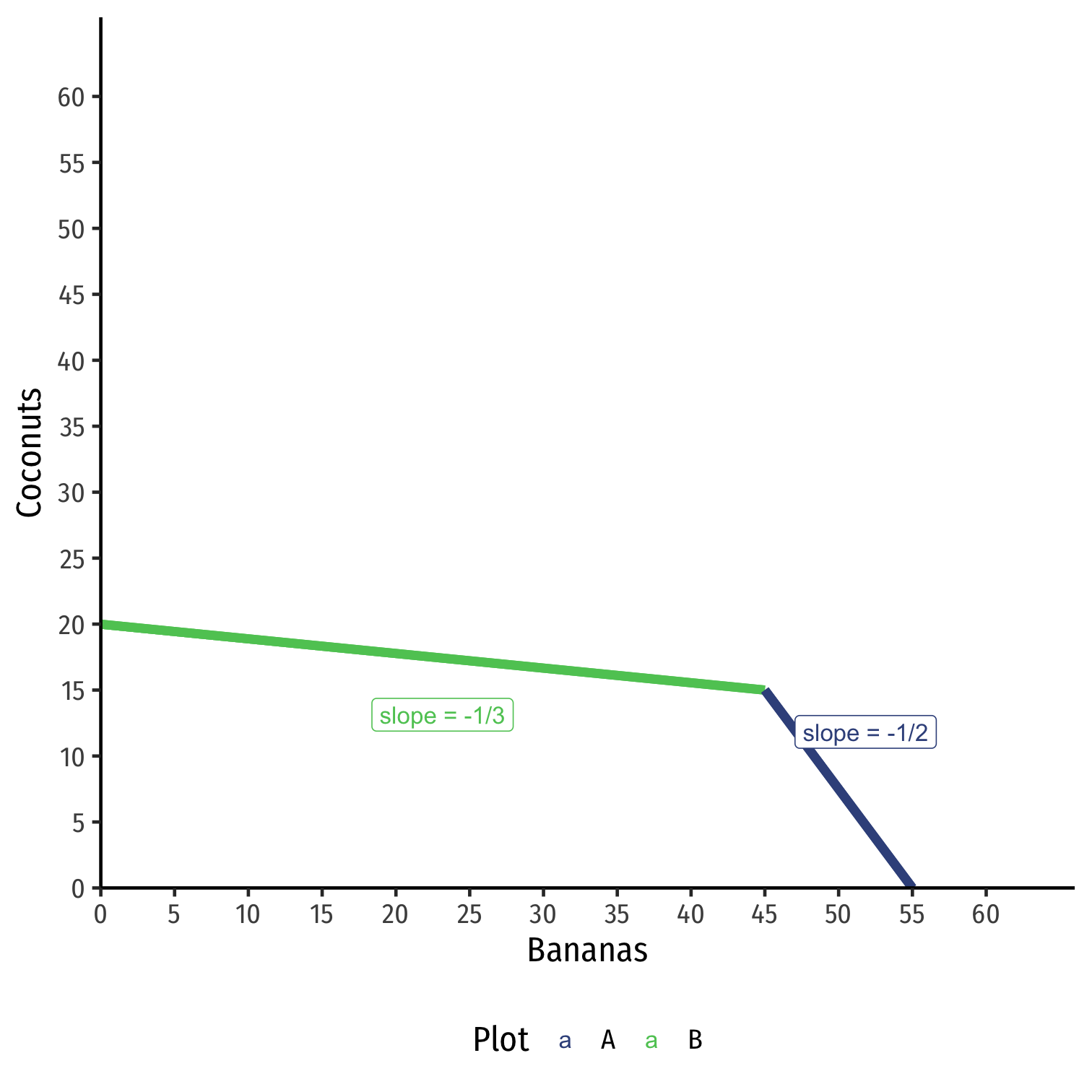
# Production, Specialization, & Comparative Advantage

- Increasing marginal cost: to produce more of a good, opportunity cost rises as he cultivates more plots of land

- Producing **Bananas** (x-axis), start with most productive plot first (.green[B]), then start cultivation on (.blue[A])
  - .hi-turquoise[“Intensive margin”]: producing more using first (most productive) plot
  - .hi-orange[“Extensive margin”]: bringing new plots into cultivation for production

]

]

---

# Production, Specialization, & Comparative Advantage

- Imagine now there are *many* various plots of land, differing in quality

- So a more-fully curved .blue[PPF]

]

<img src="2.1-slides_files/figure-html/unnamed-chunk-3-1.png" width="504" style="display: block; margin: auto;" />
]

---

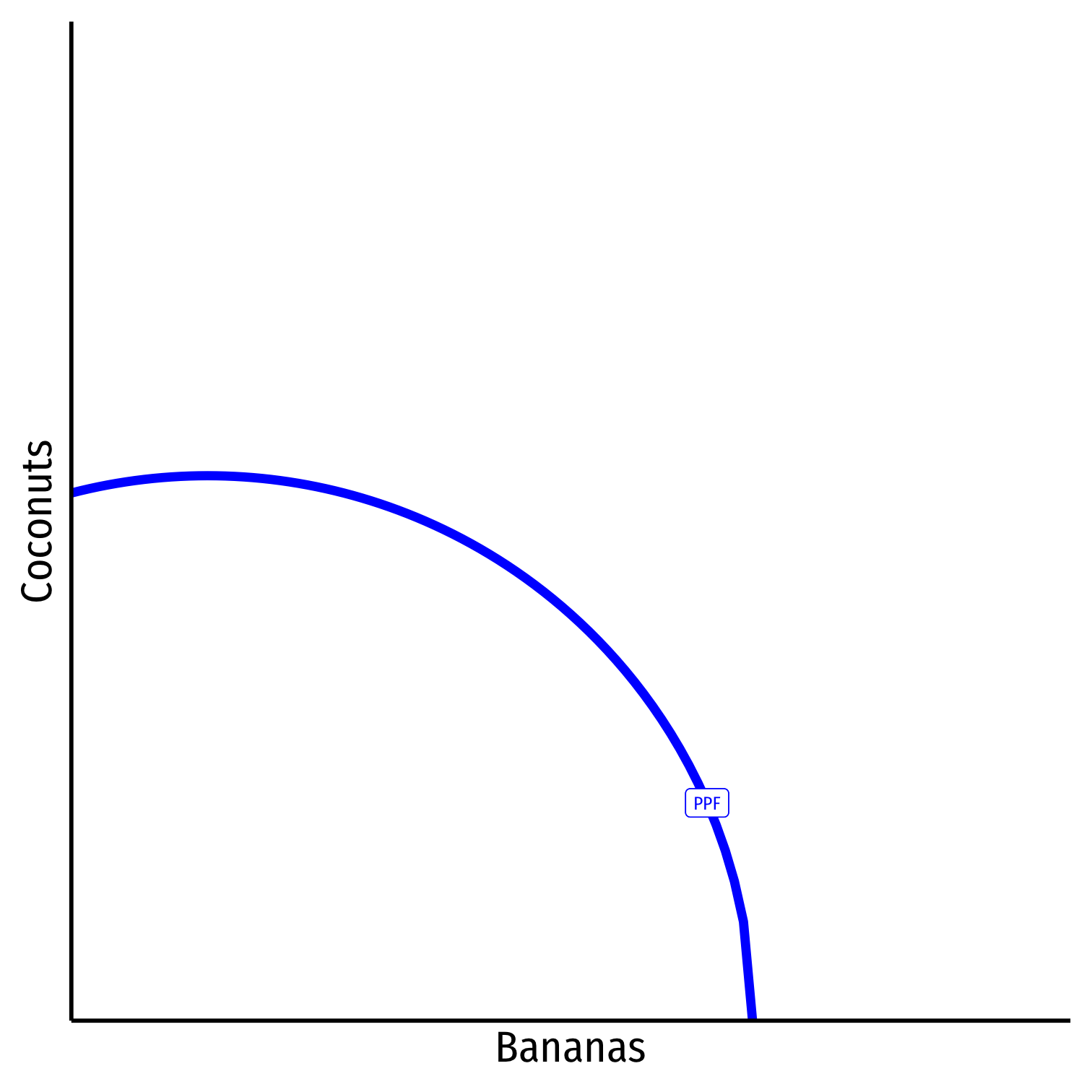
# Production, Specialization, & Comparative Advantage

- Imagine now there are *many* various plots of land, differing in quality

- So a more-fully curved .blue[PPF]

- Again, **increasing marginal cost** with more production (worse land)
  - Producing more *Bananas*, `$(A \rightarrow B)$`, slope gets *steeper*
  - Producing more *Coconuts*, `$(A \leftarrow B)$`, slope gets *flatter*

]

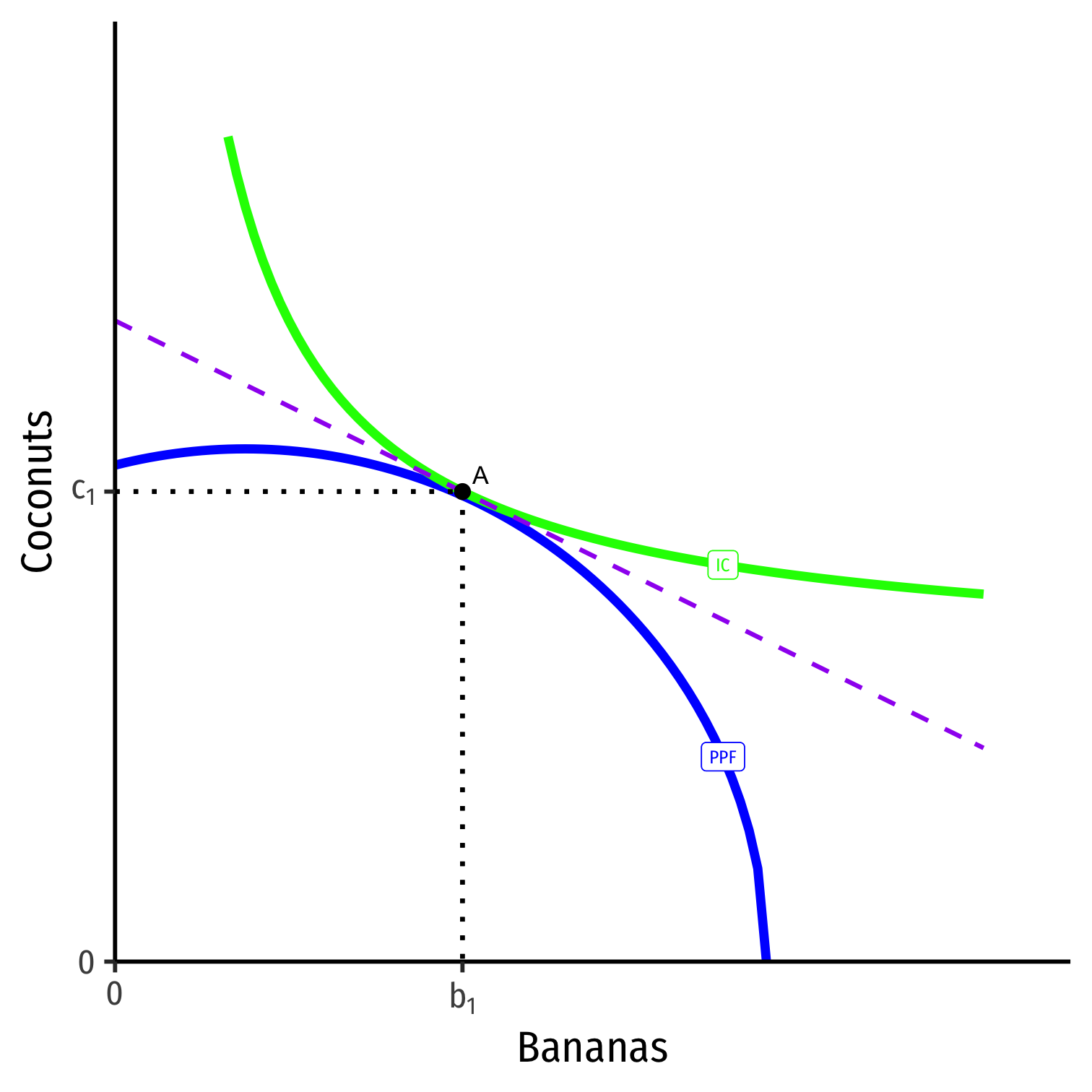
<img src="2.1-slides_files/figure-html/unnamed-chunk-4-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Production, Specialization, & Comparative Advantage

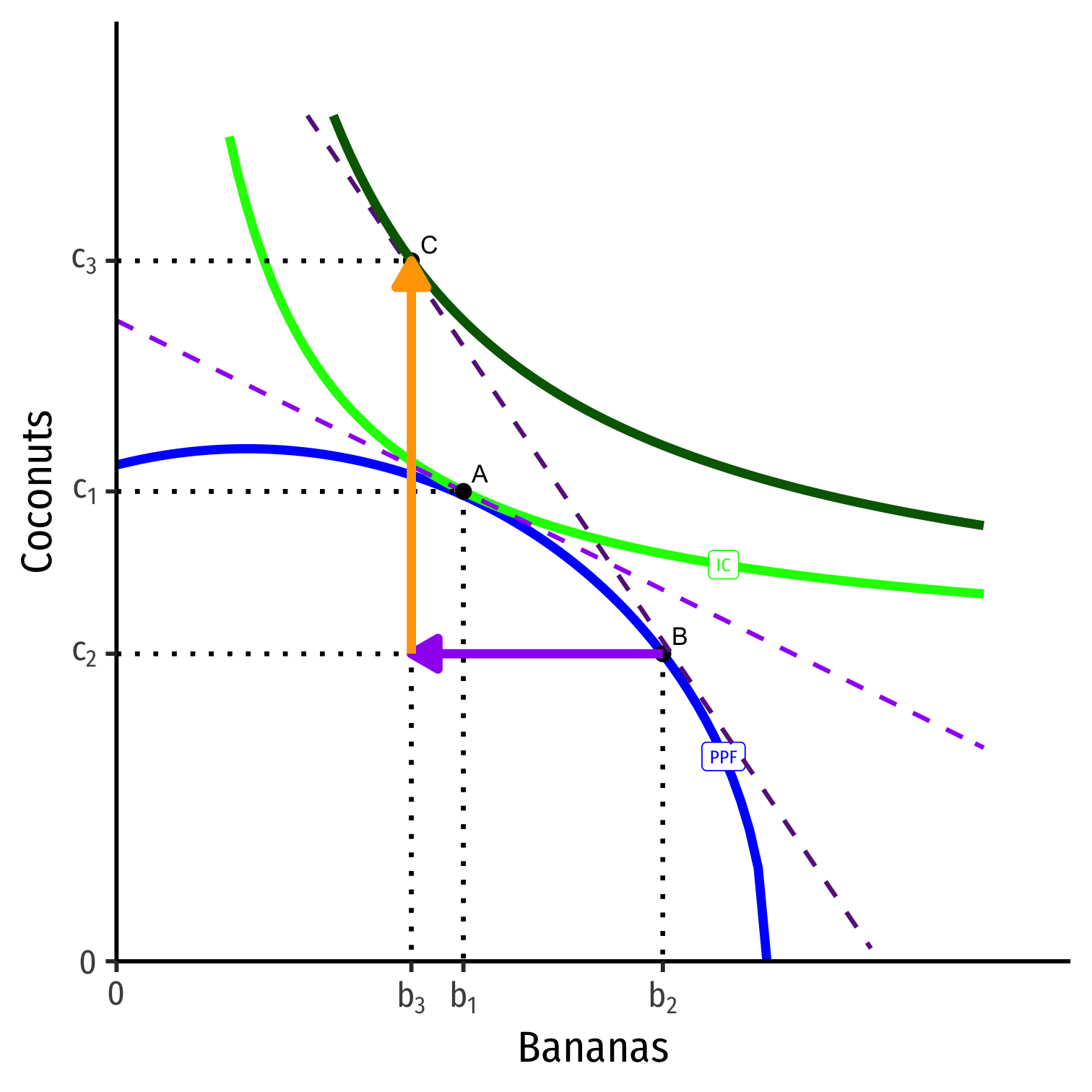
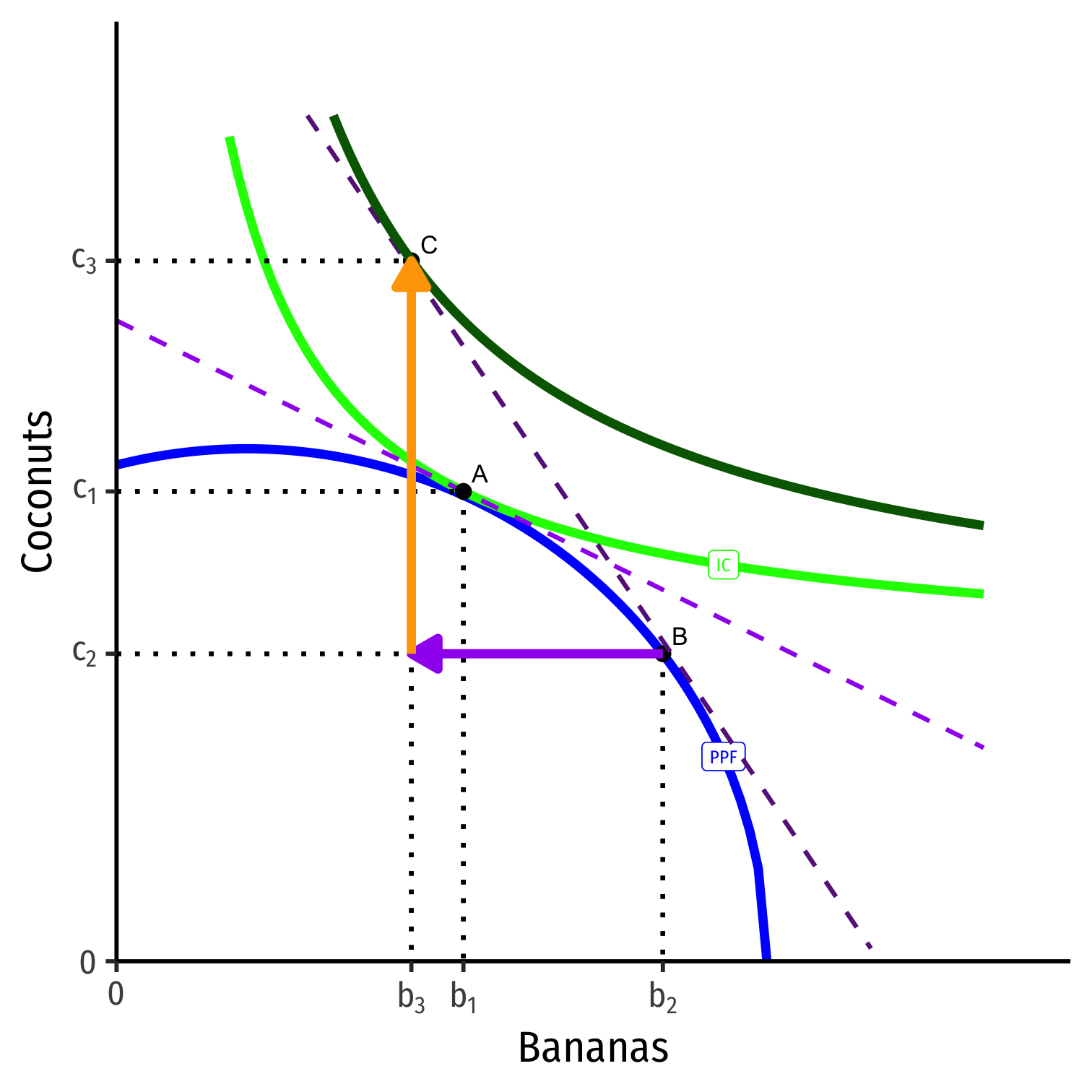
- Based on his preferences, his productive & consumption .hi[optimum] is point A (highest .green[Indifference curve] tangent to .blue[PPF])

- At this point:
`$$\underbrace{\color{blue}{MRT}}_{\text{PPF slope}}=\underbrace{\color{green}{MRS}}_{\text{I.C. slope}}=\underbrace{\color{purple}{\frac{p_b}{p_c}}}_{\text{price line}}$$`

]

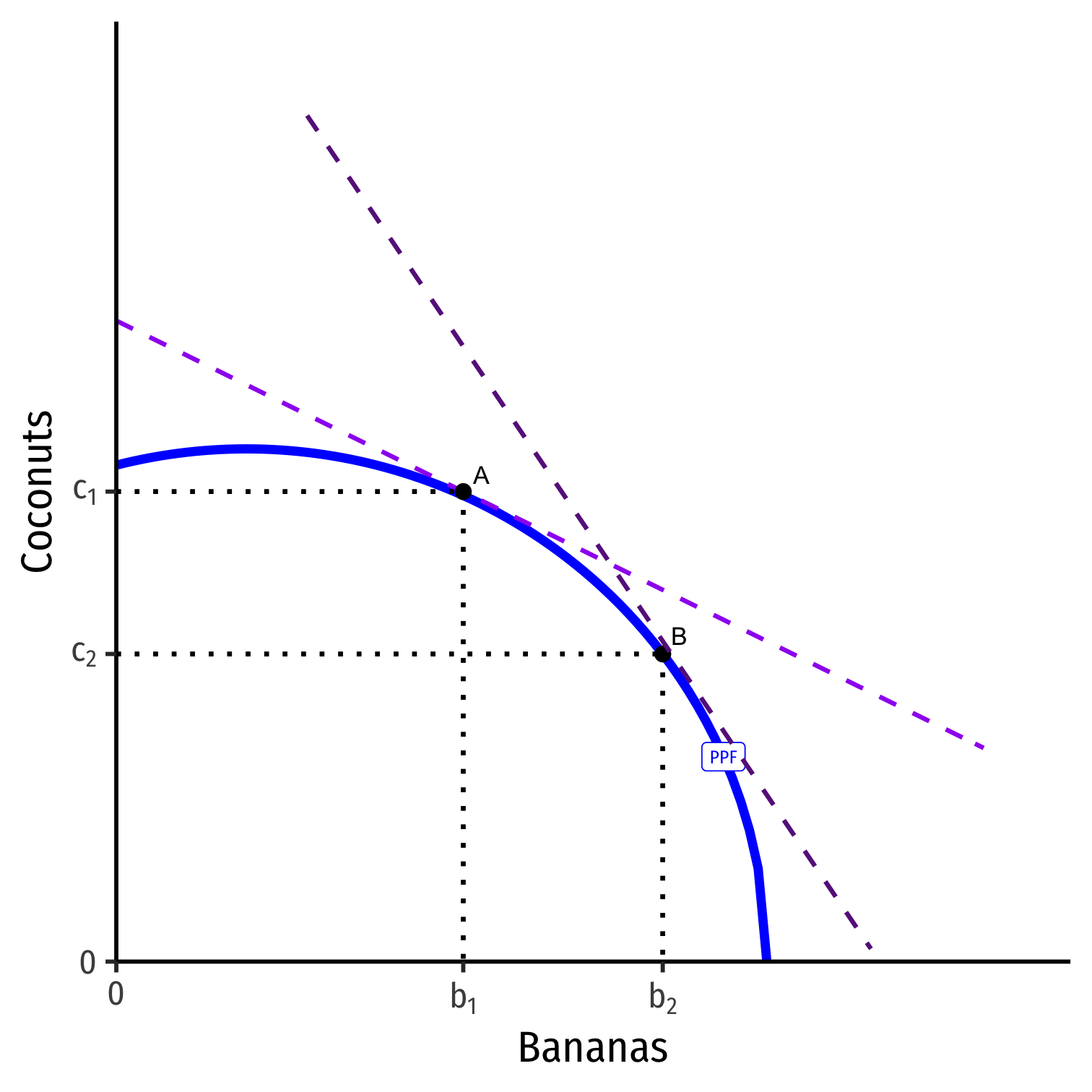
<img src="2.1-slides_files/figure-html/unnamed-chunk-5-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Trade

- Now suppose he has the opportunity to trade with others

- Current market exchange rate is the slope of darker purple dashed line

]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-6-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Trade

- Now suppose he has the opportunity to trade with others

- Current market exchange rate is the slope of darker purple dashed line

- He will .hi[specialize] in production of Bananas, produce more of them `$(A \rightarrow B)$` to trade to get coconuts
  - B is his .hi[productive optimum]
]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-7-1.png" width="504" style="display: block; margin: auto;" />
]

---

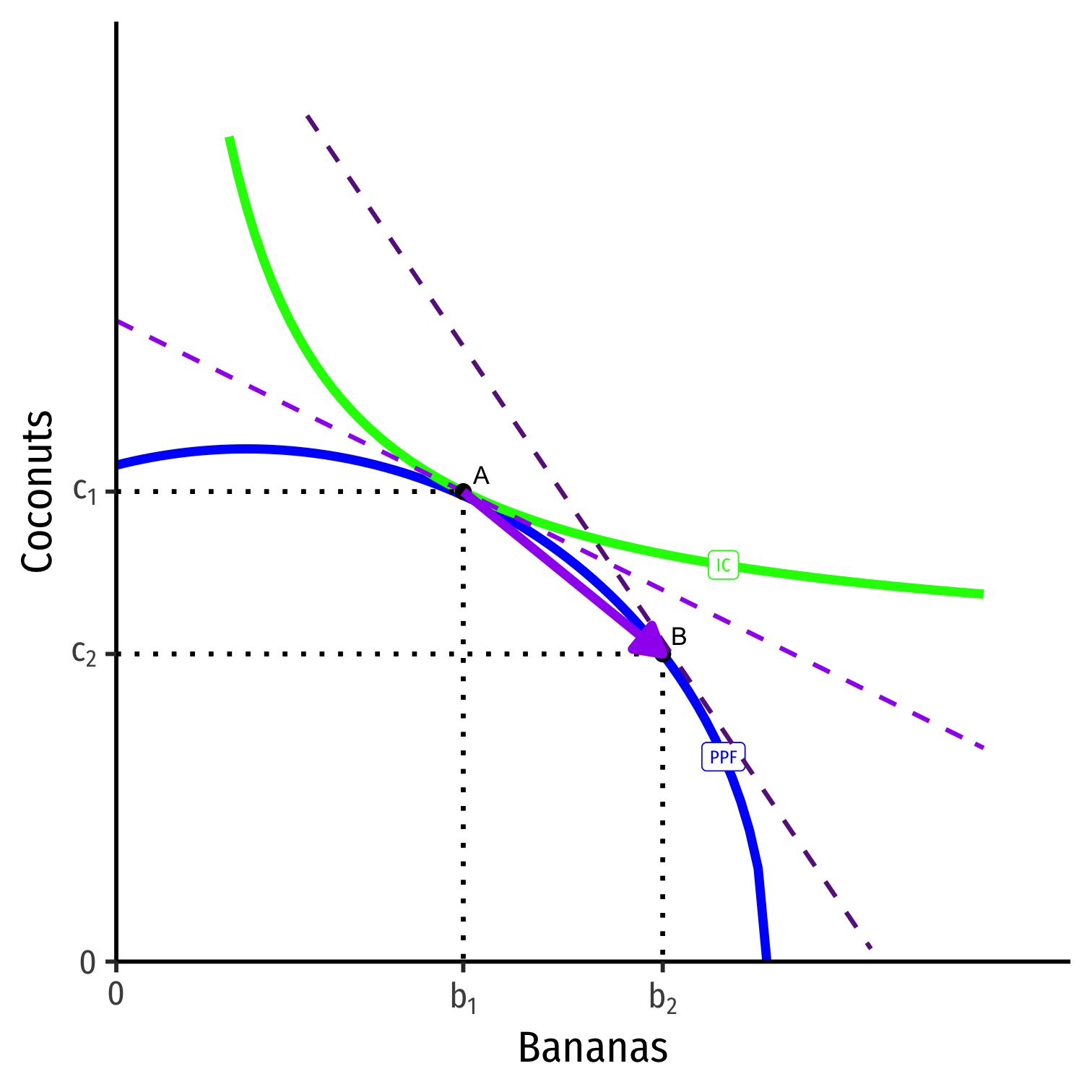
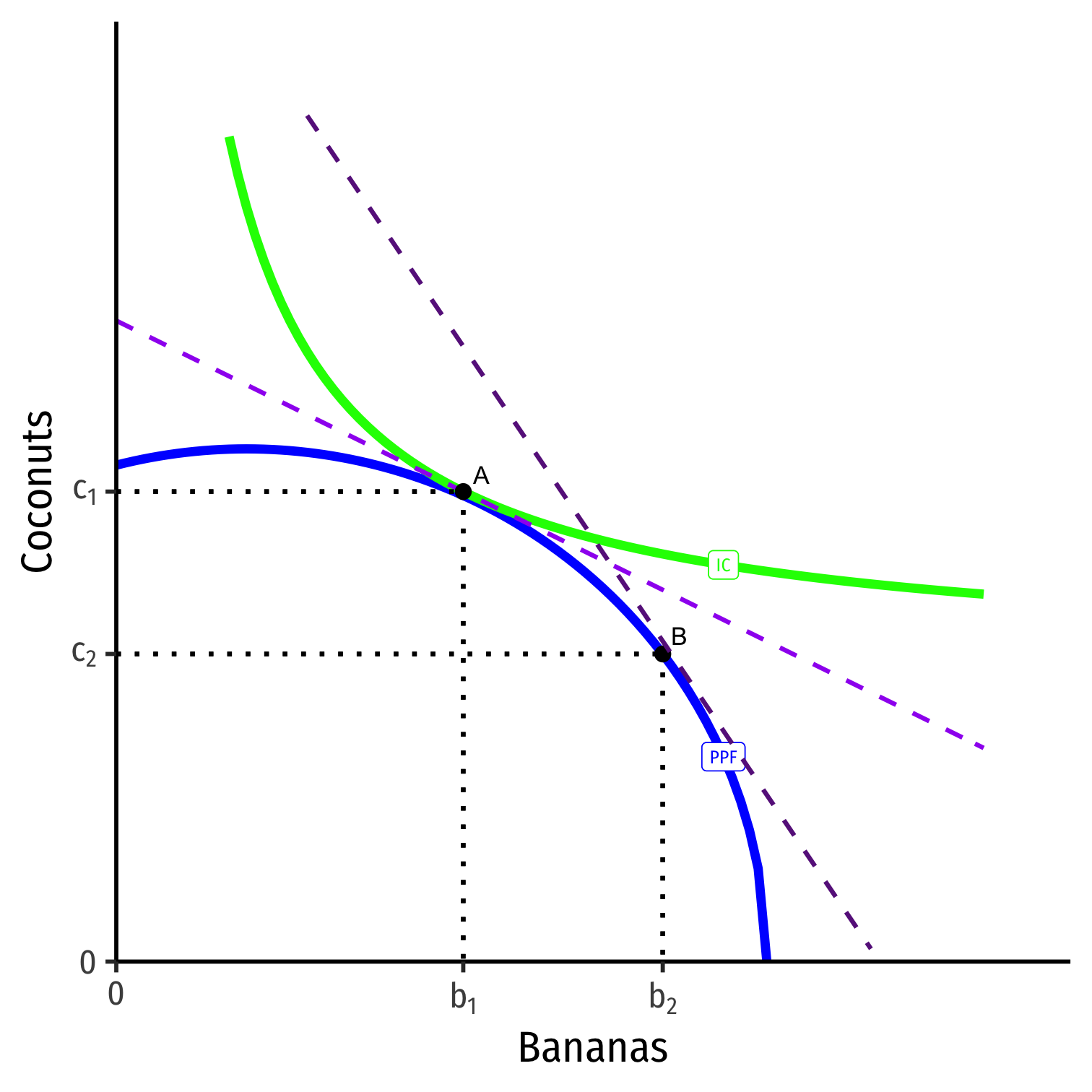
# Post-Trade Consumption

- He will trade at the market prices (slope of dark purple dashed line)

]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-8-1.png" width="504" style="display: block; margin: auto;" />
]

---

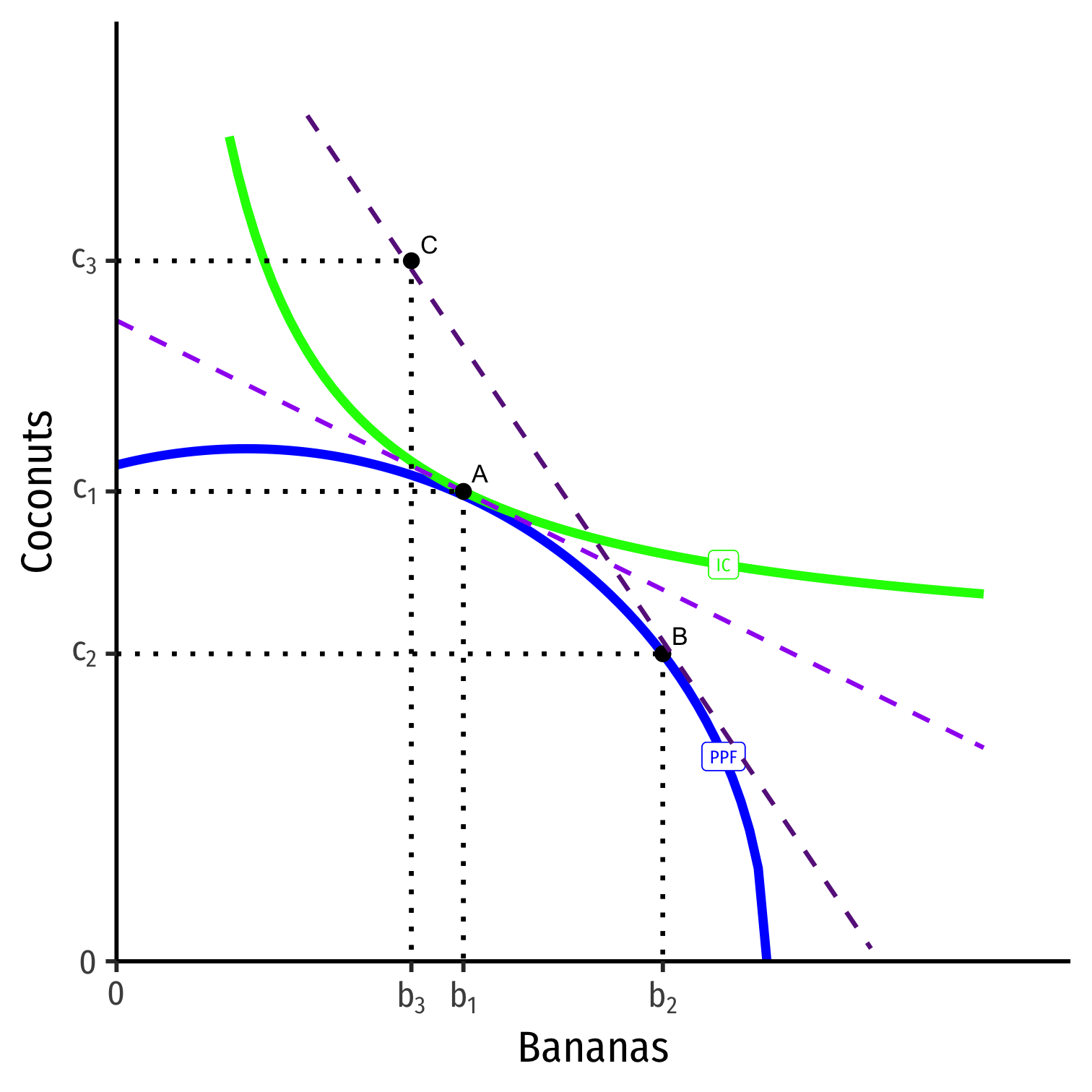
# Post-Trade Consumption

- He will trade at the market prices (slope of dark purple dashed line)
  - Sell (export) his specialized good, Bananas

]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-9-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Post-Trade Consumption

- He will trade at the market prices (slope of dark purple dashed line)
  - Sell (export) his specialized good, Bananas
  - Buy (import) from others, Coconuts

]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-10-1.png" width="504" style="display: block; margin: auto;" />
]

---

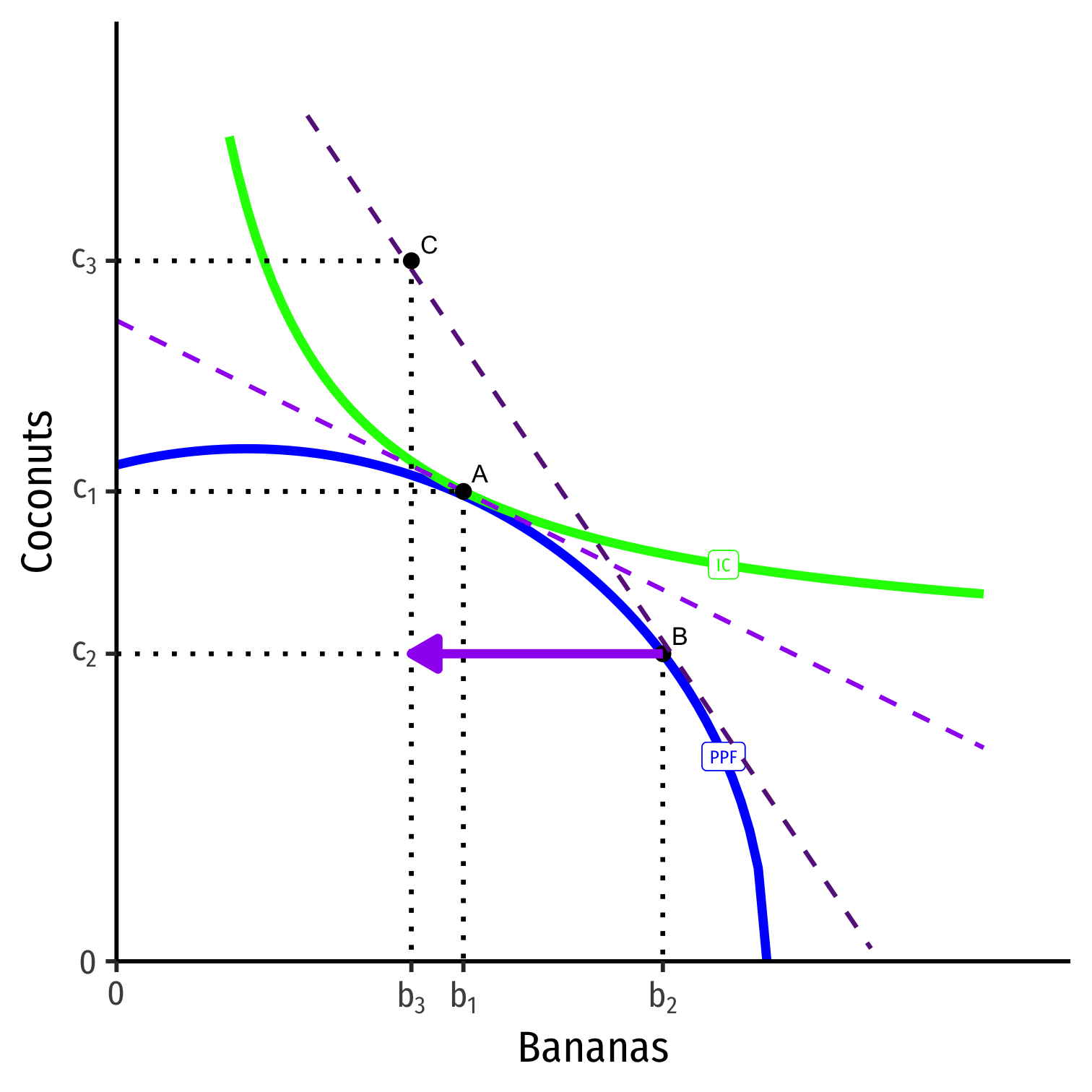
# Post-Trade Consumption

- He will trade at the market prices (slope of dark purple dashed line)
  - Sell (export) his specialized good, Bananas
  - Buy (import) from others, Coconuts

- Allows him to reach higher .green[indifference curve] at point C, new .hi[consumption optimum]

]

.pull-right[
<img src="2.1-slides_files/figure-html/trade-1.png" width="504" style="display: block; margin: auto;" />
]

---

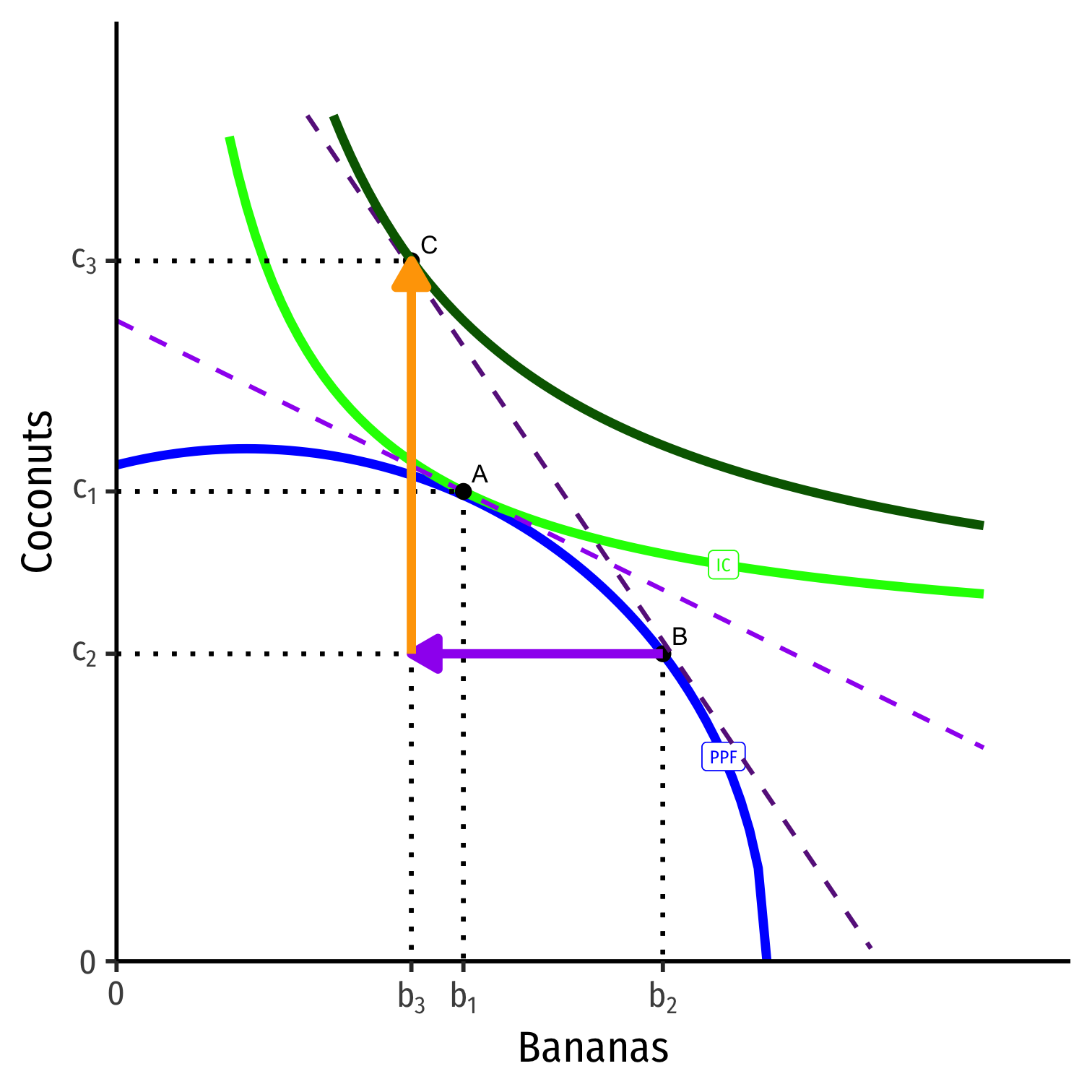
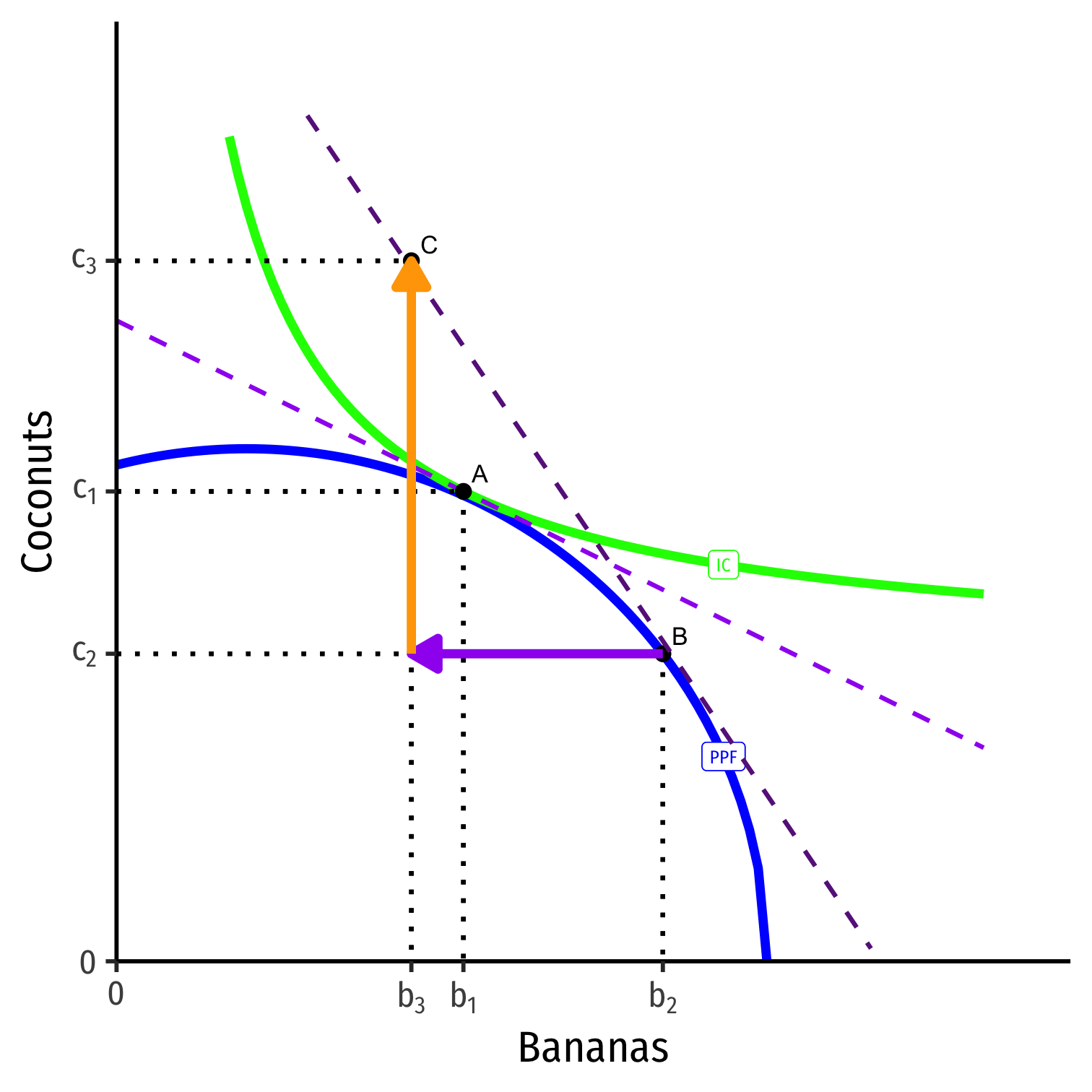
# Takeaways

1. .hi-purple[Trade is good]
  - Reaches higher indifference curve, beyond PPF!

]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-11-1.png" width="504" style="display: block; margin: auto;" />
]

---

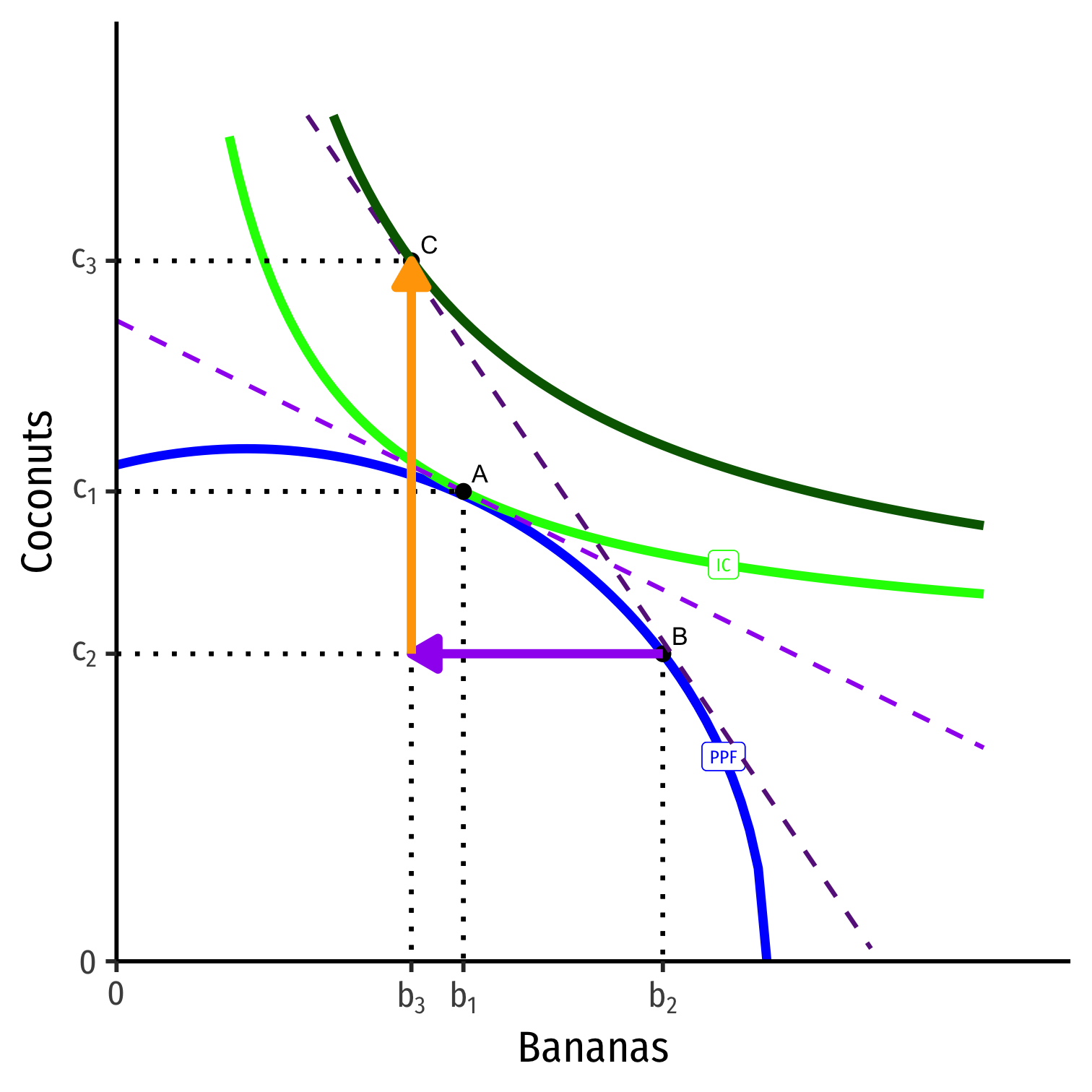
# Takeaways: Comparative Advantage

1. Trade is good

2. .hi[Specialization] and .hi[Comparative advantage]
  - specialize in producing whatever good you have the lower opportunity cost in
  - buy (import) everything else!
  - can be comparatively good at something, or comparatively bad at everything else!
]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-12-1.png" width="504" style="display: block; margin: auto;" />
]

---

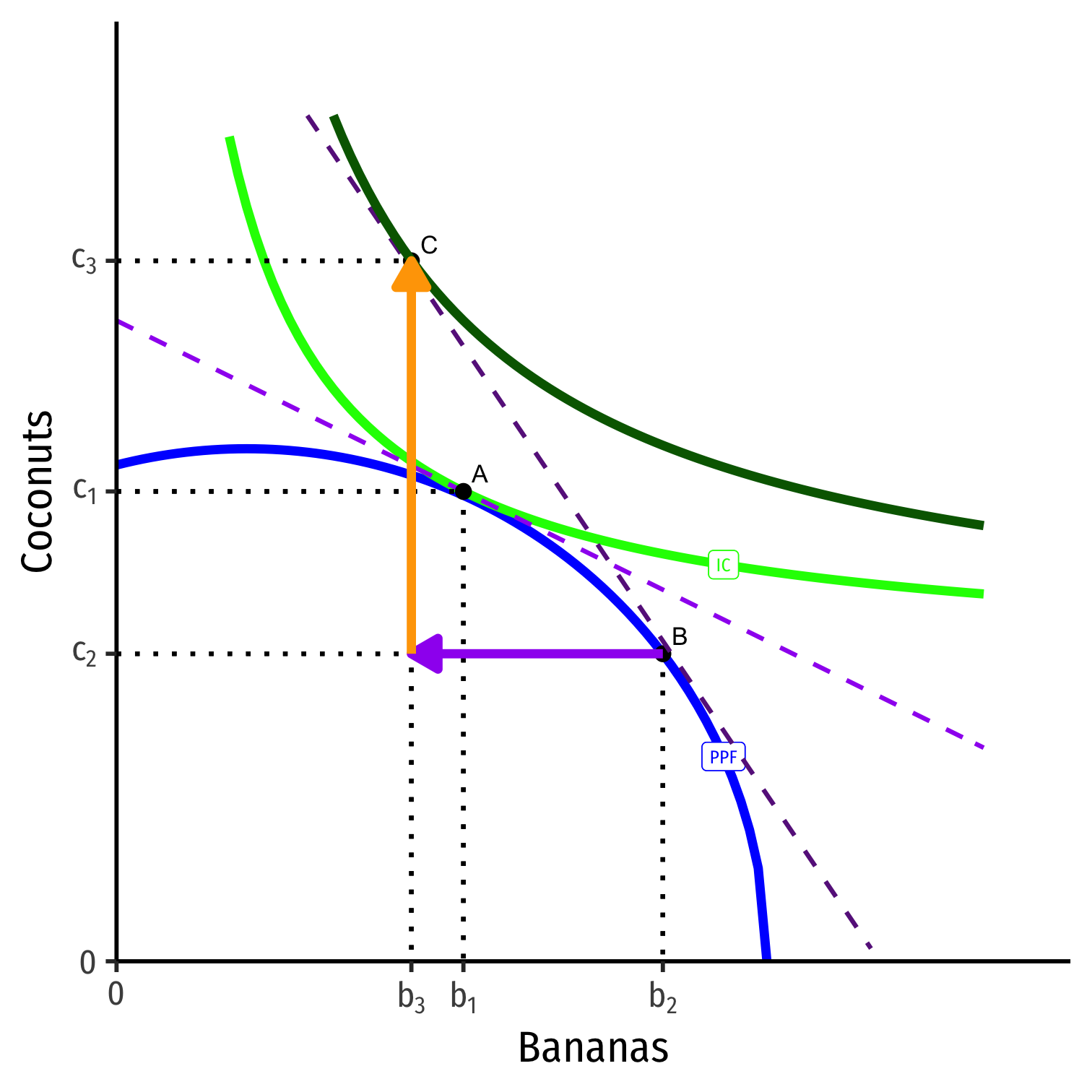
# Takeaways: Comparative Advantage

---

# Takeaways: Comparative Advantage

---

# The Division of Labor

Adam Smith

1723-1790
]
]

> "The greatest improvement in the productive powers of labour, and the greater part of the skill, dexterity, and judgment with which it is any where directed, or applied, seem to have been the effects of the **division of labour**," (Book I, Chapter 1).
]

.source[Smith, Adam, 1776, [*An Enquiry into the Nature and Causes of the Wealth of Nations*](https://www.econlib.org/library/Smith/smWN.html)]

---

# Takeaways: Comparative Advantage

- Learn much more in my [international trade](https://tradef20.classes.ryansafner.com) course
]
]
.pull-right[
.center[
![:scale 80%](../images/trade_hex.png)
]
]

---

# Takeaways

.pull-left[
.smaller[
1. Trade is good
2. Specialization and comparative advantage
3. .hi-purple[Price differences imply gains from trade]
  - different price lines in “autarky” vs. with trade
  - the more different his price is vs. market, the better off he will be!
]
]

.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-13-1.png" width="504" style="display: block; margin: auto;" />
]

---

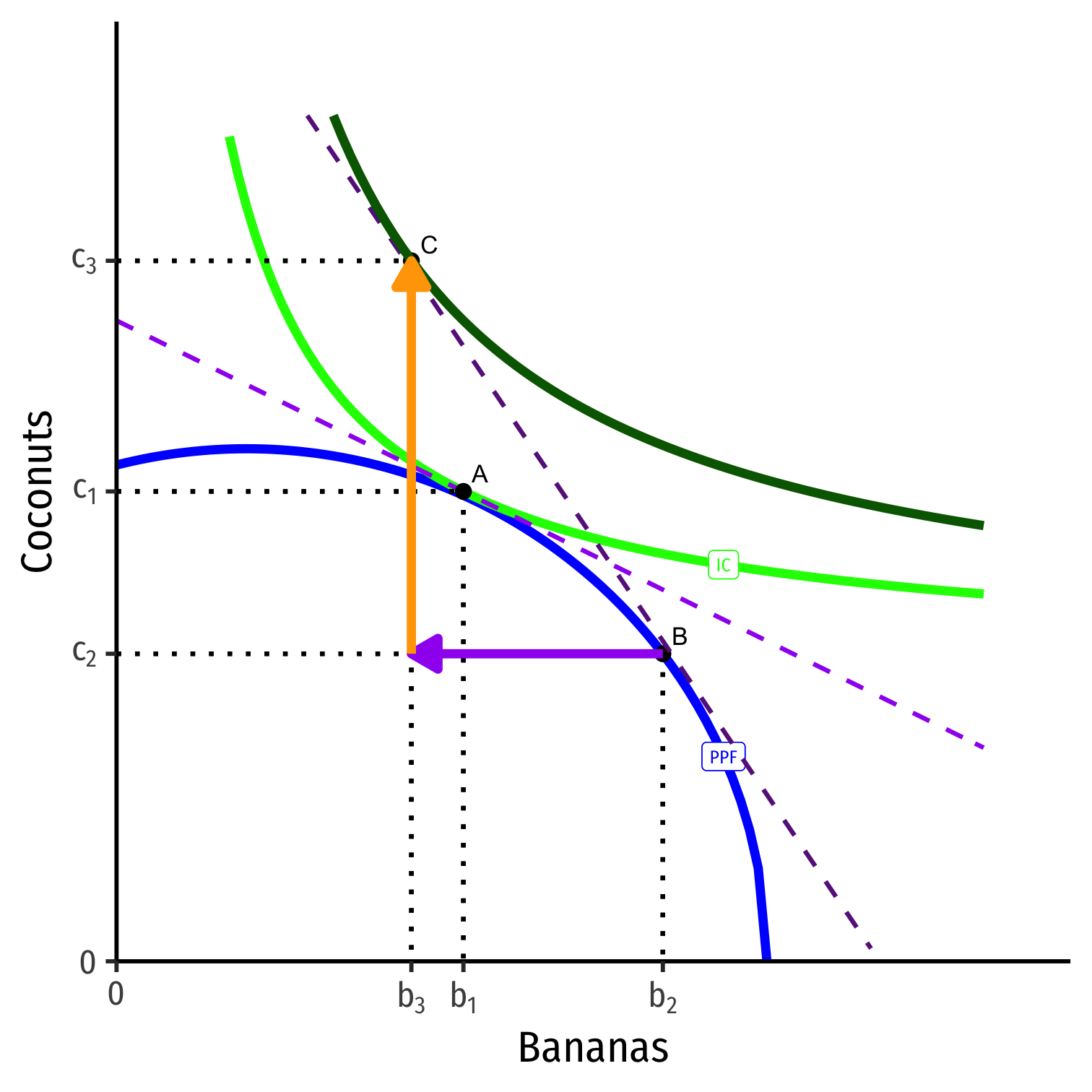
# Takeaways

.pull-left[
.smaller[
1. Trade is good
2. Specialization and comparative advantage
3. Price differences imply gains from trade
4. A .hi[theory of the firm]
 - Productive optimum (B) is independent of preferences!
 - *Any* rational producer would make the same decision, regardless of preferences (or ownership structure)
 - sole-proprietor, partnership, corporation, non-profit, workers co-op, etc.
]
]
.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-14-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Takeaways

.pull-left[
.smaller[
1. Trade is good
2. Specialization and comparative advantage
3. Price differences imply gains from trade
4. A theory of the firm
5. .hi[Competitive firms produce where MC = MB]
  - Point B:
  
`$$\underbrace{\color{blue}{MRT}}_{\text{PPF slope}}=\underbrace{\color{green}{MRS}}_{\text{I.C. slope}}=\underbrace{\color{purple}{\frac{p_b}{p_c}}}_{\text{price line}}$$`

]
]
.pull-right[
<img src="2.1-slides_files/figure-html/unnamed-chunk-15-1.png" width="504" style="display: block; margin: auto;" />
]

---

# What Do Firms Do?

---

# The Firm

.pull-left[
- In modern market economies, most production takes place in a legal organization known as .hi[the firm]

- It does not *have* to be this way, and for most of history it was not this way!
    - Craft guilds
    - Independent artisans
    - Independent contractors

]

---

# The Firm

.pull-left[
.smaller[
- Firms exist in the forms they do because they are an efficient response to particular problems of economic organization

- Lots of interesting, Nobel-prize winning, analysis

- For now, we'll sidestep these and just *assume* firms exist. Learn more in my .hi[Industrial Organization] course:
  - [Why Are There Firms?](https://ios20.classes.ryansafner.com/class/3.1-class/)
  - [The Firm as Nexus of Contracts](https://ios20.classes.ryansafner.com/class/3.2-class/)
  - [Asset Specificity and Vertical Integration](https://ios20.classes.ryansafner.com/class/3.3-class/)
  - [Contractual Restraints & Property Rights](https://ios20.classes.ryansafner.com/class/3.4-class/)

]
]

---

# What Do Firms Do? I

- We'll assume "the firm" is the agent to model:

- So what do firms do?

- How would we set up an optimization model:

1. **Choose:** .hi-blue[ < some alternative >]

2. **In order to maximize:** .hi-green[< some objective >]

3. **Subject to:** .hi-red[< some constraints >]

]

---

# What Do Firms Do? II

---

# What Do Firms Do? II

---
# What Do Firms Do? II

- **Inputs**: `$x_1, x_2, \cdots, x_n$`
 - **Examples**: worker efforts, warehouse space, electricity, loans, oil, cardboard, fertilizer, computers, software programs, etc
 
- **Output**: `$q$`
 - **Examples**: gas, cars, legal services, mobile apps, vegetables, consulting advice, financial reports, etc
]
]

---

# What Do Firms Do? III

.pull-left[
- .hi[Technology] or a .hi[production function]: rate at which firm can convert specified inputs `$(x_1, x_2, \cdots, x_n)$` into output `$(q)$`
`$$q=f(x_1, x_2, \cdots, x_n)$$`

]

---

# Production Function as Recipe

![](../images/recipe1.PNG)
]
]

![](../images/recipe2.PNG)
]

]

---

# Factors of Production I

`$$q=A \,f(t,l,k)$$`

.pull-left[
.smaller[
- Economists typically classify inputs, called the .hi[“factors of production” (FOP)]:

<table>
 <thead>
 <tr>
 <th style="text-align:left;"> Factor </th>
 <th style="text-align:left;"> Owned By </th>
 <th style="text-align:left;"> Earns </th>
 </tr>
 </thead>
<tbody>
 <tr>
 <td style="text-align:left;"> Land (t) </td>
 <td style="text-align:left;"> Landowners </td>
 <td style="text-align:left;"> Rent </td>
 </tr>
 <tr>
 <td style="text-align:left;"> Labor (l) </td>
 <td style="text-align:left;"> Laborers </td>
 <td style="text-align:left;"> Wages </td>
 </tr>
 <tr>
 <td style="text-align:left;"> Capital (k) </td>
 <td style="text-align:left;"> Capitalists </td>
 <td style="text-align:left;"> Interest </td>
 </tr>
</tbody>
</table>
]
.smallest[
- `$A$`: .b["total factor productivity"] (ideas/knowledge/institutions)
- and Entrepreneurs/Owners who earn .b[Profit]

]
]
.pull-right[
.center[
![](../images/factors.jpg)
]

]

---

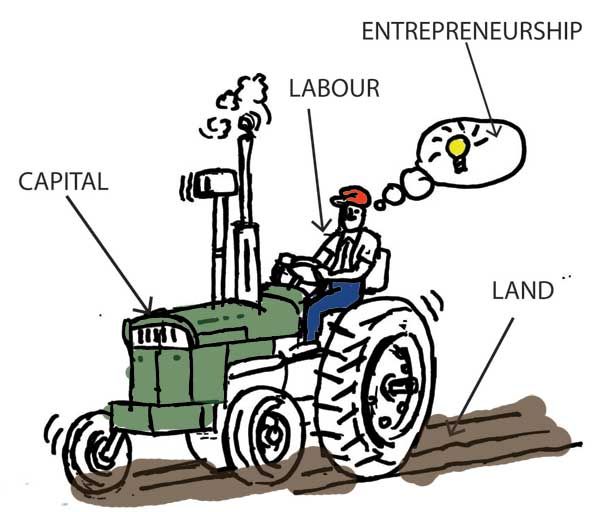
# Factors of Production II

`$$q=f(l,k)$$`

- We will assume just two inputs: labor `$l$` and capital `$k$`

]

]

---

# What Does a Firm Maximize?

- We will assume firms .hi-purple[maximize profit `\$(\pi)\$`]

- Not true for all firms
 - **Examples**: non-profits, charities, civic associations, government agencies, criminal organizations, etc

- Even profit-seeking firms may also want to maximize additional things
 - **Examples**: goodwill, sustainability, social responsibility, etc

]

---

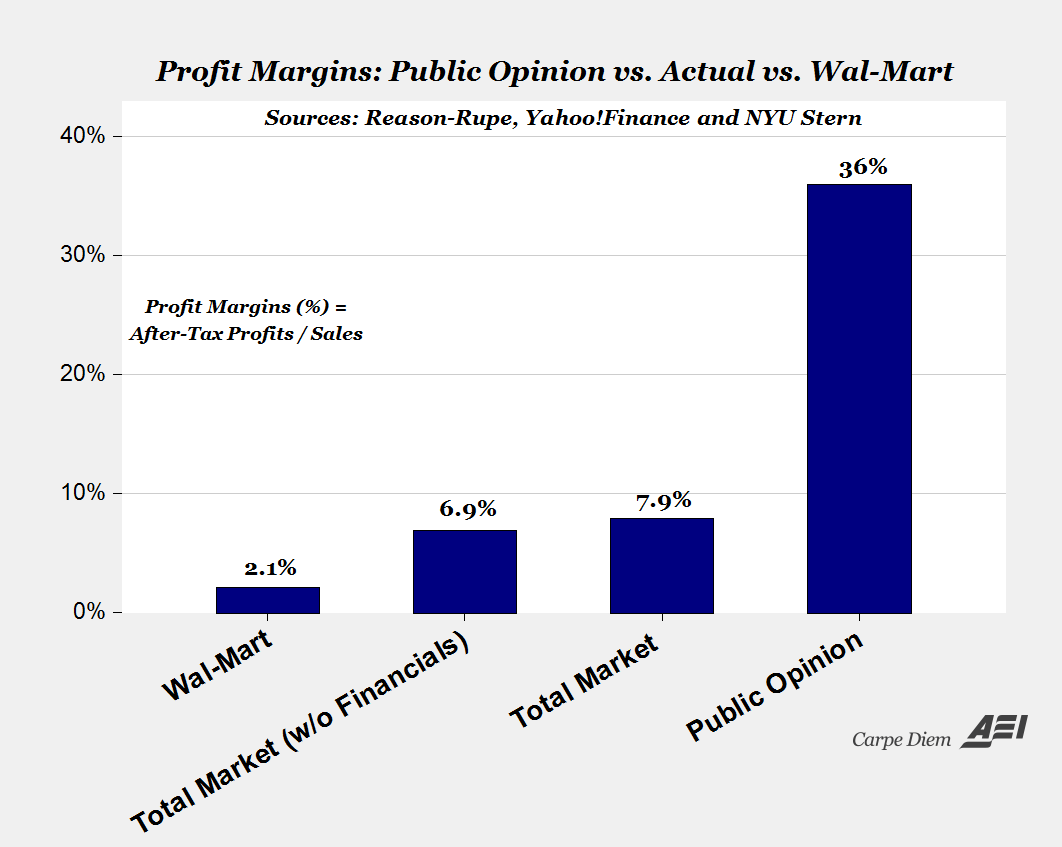
# Profits Have a Bad Rap These Days

---

# What is Profit?

- In economics, profit is simply **benefits minus (opportunity) costs**

]

---

# What is Profit?

- In economics, profit is simply **benefits minus (opportunity) costs**

- Suppose firm sells **output** `$q$` at price `$p$`

]

---

# What is Profit?

- In economics, profit is simply **benefits minus (opportunity) costs**

- Suppose firm sells **output** `$q$` at price `$p$`

- It can buy each **input** `$x_i$` at an associated price `$p_i$`
    - labor `$l$` at wage rate `$w$`
    - capital `$k$` at rental rate `$r$`

]

---

# What is Profit?

- In economics, profit is simply **benefits minus (opportunity) costs**

- Suppose firm sells **output** `$q$` at price `$p$`

- It can buy each **input** `$x_i$` at an associated price `$p_i$`
    - labor `$l$` at wage rate `$w$`
    - capital `$k$` at rental rate `$r$`

- The profit of selling `$q$` units and using inputs `$l,k$` is:

]

---

# Who Gets the Profits? I

]

---

# Reminder from Macroeconomics: "The Circular Flow"

---

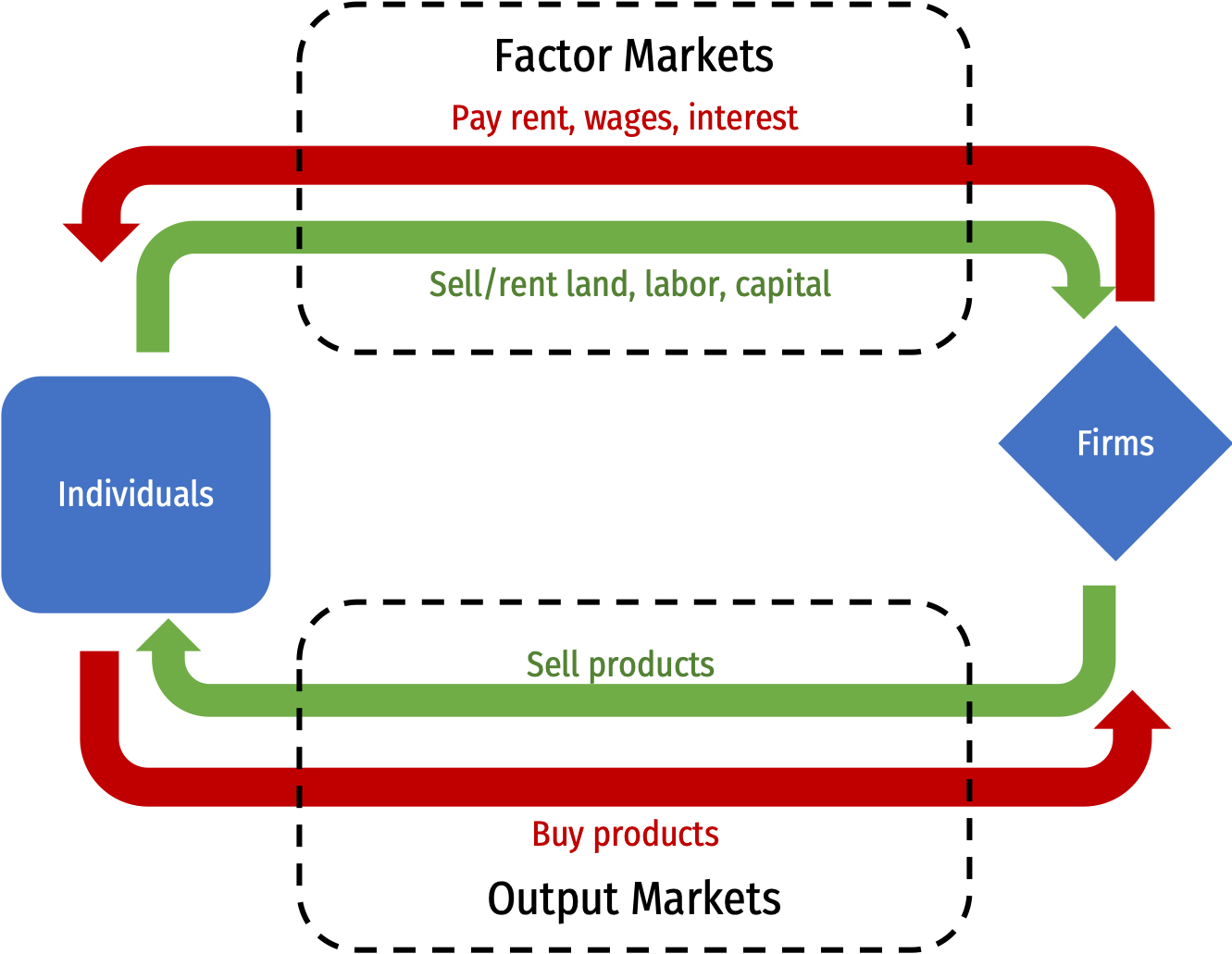
# Who Gets the Profits? I

- .hi-purple[The firm's costs are all of the factor-owner's incomes!]
    - Landowners, laborers, creditors are all paid rent, wages, and interest, respectively

]

---

# Who Gets the Profits? I

- Profits are the .hi-purple[residual value] leftover after paying all factors

- Profits are income for the .hi[residual claimant(s)] of the production process (i.e. **owner(s)** of a firm):
    - Entrepreneurs
    - Shareholders

]

---

# Who Gets the Profits? II

- Residual claimants have incentives to maximize firm's profits, as this *maximizes their own income*

- Entrepreneurs and shareholders are the only participants in production that are *not* guaranteed an income!
    - Starting and owning a firm is inherently **risky**!

]

# People Overestimate Profits

.source[Source: [American Enterprise Institute](https://www.aei.org/carpe-diem/the-public-thinks-the-average-company-makes-a-36-profit-margin-which-is-about-5x-too-high-part-ii/)]

---

# Profits and Entrepreneurship: A Preview

- In markets, production must face the .hi[profit test]:
 - Is consumer's willingness to pay `$>$` opportunity cost of inputs?

- Profits are an indication that **value is being created for society**

- Losses are an indication that **value is being destroyed for society**

- Survival in markets *requires* firms continually create value & earn profits
]

---

# The Firm's Optimization Problem I

- So what do firms do?

1. **Choose:** .hi-blue[ < some alternative >]

2. **In order to maximize:** .hi-green[< profits >]

3. **Subject to:** .hi-red[< technology >]

- We've so far assumed they maximize profits and they are limited by their technology

]

---

# The Firm's Optimization Problem II

- Prices?
 - Depends on the market the firm is operating in!
 - Study of industrial organization
 
- Essential question: how competitive is a market? This will influence what firms (can) do
]

---

# Industrial Organization: A Roadmap I

- Begin with one extreme case: .hi["perfect competition"]
  - Firms can choose to sell as much `$q^*$` as they want
  - Firms are constrained to sell at the (exogenous) market price `$\bar{p}$`

- Appropriate for settings with *many* firms, each small relative to market
]

# Interlude

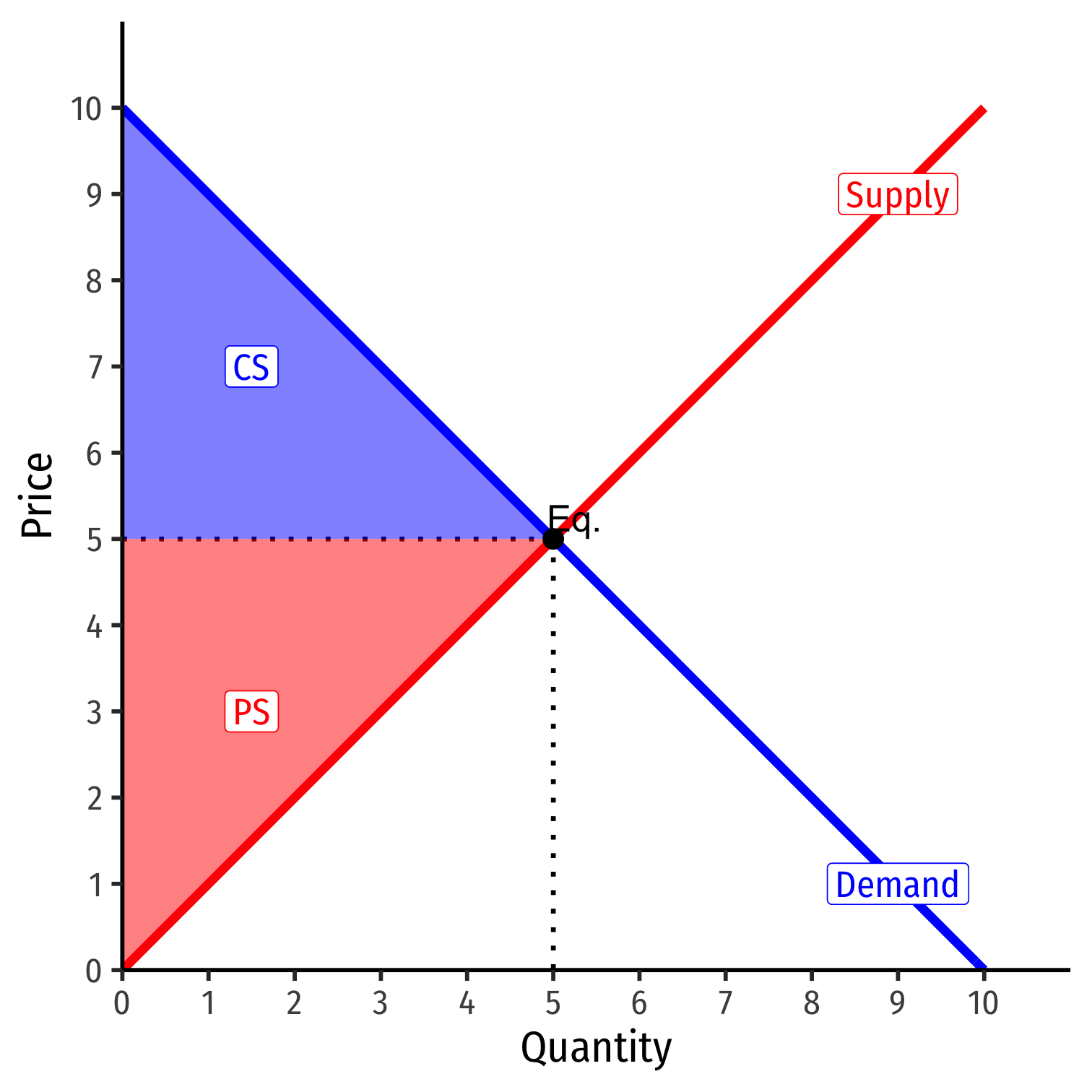
- After we find firm's **optimal decisions** in this market (and have Exam 2), we will then finally look at **market equilibrium**

- Put Supply and Demand together
]

]

---

# Interlude

- We've seen how **consumers** cause and respond to market changes
  - e.g. `$(\Delta p_x$`, `$\Delta p_y$`, `$\Delta m$`)
  
- We're about to explore how **producers** cause and respond to market changes

- Finally we can explain all of these market changes with Supply and Demand .hi[equilibrium models]

- Discuss how markets work, why they are good & efficient, and when they fail
]

]

---

# Industrial Organization: A Roadmap II

.pull-left[
- Examine another extreme case: .hi[monopoly] of a single seller
    - Appropriate for some markets

- .hi-purple["Imperfect competition"]: models of .hi[monopolistic competition] & .hi[oligopoly]
 - In latter case, firms act **strategically**, so we will need game theory
 
- Firms can choose *both* `$q^*$` & `$p^*$` to maximize `$\pi$`

]